题目内容

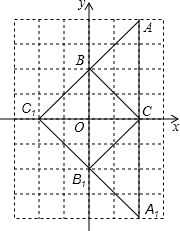如图，方格纸中的每个小方格都是边长为1个单位的正方形．已知△ABC的顶点均在格点上，建立直角坐标系后，点A的坐标为（2，4）．
（1）直接写出点B，C，B₁，A₁的坐标；
（2）△A₁B₁C可以看作是由△ABC经过怎样的变换得到，写出变换过程；
（3）作△B B₁C关于y轴对称的图形，点C的对称点为C₁，请直接写出△AC₁A₁的形状．

解：（1）结合直角坐标系可得：B（0，2）、C（2，0）、B₁（0，-2）A₁（2，-4）；

（2）本题答案不唯一：
方法一：对称变换：△A₁B₁C可以看作是由△ABC作关于x轴的轴对称变换得到．
方法二：平移变换：△A₁B₁C可以看作是由△ABC向下平移4个单位得到．
方法三：-旋转变换：△A₁B₁C可以看作是由△ABC绕点C逆（或顺）时针旋转180°得到；

（3）如图：
△AC₁A₁为等腰直角三角形．
分析：（1）结合直角坐标系即可得出各点坐标；
（2）结合图形即可作出判断（答案不唯一）
（3）结合图形可判断△AC₁A₁的形状．
点评：本题考查了轴对称作图的知识，属于基础题，解答本题的关键是结合图形及直角坐标系进行判断．

练习册系列答案

语文阅读训练系列答案

点对点决胜中考系列答案

填充练习册系列答案

阅读导航系列答案

教材3D解读系列答案

通城学典默写能手系列答案

新中考仿真试卷系列答案

毕业总复习高分策略指导与实战训练系列答案

创优考100分系列答案

高分中考系列答案

相关题目

22、如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点C的坐标为（2，-1）．
（1）把△ABC先向上平移4个单位得△A₁B₁C₁，再沿x轴翻折得△A₂B₂C₂，请在网格中画出△A₂B₂C₂，并写出C₂的坐标．
（2）以原点为位似中心，在第二象限内画出△ABC的位似图形△A₃B₃C₃，且△A₃B₃C₃与△ABC的相似比为2，并写出C₃的坐标．

17、如图，方格纸中的每个小方格都是边长为1的正方形，我们把以格点间连续为边的三角形称为“格点三角形”，图中的△ABC是格点三角形，在建立平面直角坐标系后，点B的坐标为（-1，-1）把△ABC绕点C按顺时针方向旋转90°后得到△A₁B₁C，画出△A₁B₁C的图形，并写出点B₁的坐标．

16、如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点B的坐标为（-1，0）
（1）画出△ABC关于y轴对称的△A₁B₁C₁；
（2）画出将△ABC绕原点O按逆时针旋转90°所得的△A₂B₂C₂；
（3）△A₁B₁C₁与△A₂B₂C₂成轴对称图形吗？若成轴对称图形，写出对称轴．

如图，方格纸中的每个小正方格都是边长为1个单位长度的正方形，每个小正方形的顶点叫格点，△ABC的顶点均在格点上，O、M都在格点上．
（1）画出△ABC关于直线OM对称的△A₁B₁C₁；
（2）画出将△ABC绕点O按顺时针方向旋转90°后得到的△A₂B₂C₂
（3）△A₁B₁C₁与△A₂B₂C₂组成的图形是轴对称图形码？如果是轴对称图形，请画出对称轴．

如图，方格纸中的每个小方格都是边长为1的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，A（-1，5），B（-1，0），C（-4，3）．
（1）画出△ABC关于y轴对称的△A₁B₁C₁；（其中A₁、B₁、C₁是A、B、C的对应点，不写画法）
（2）写出A₁、B₁、C₁的坐标；
（3）求出△A₁B₁C₁的面积．