题目内容
(本题满分10分)
已知:如图,在Rt△ABC中,∠ACB=90º,AC=6,sinB=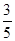 , 点D是边BC的中点,
, 点D是边BC的中点,
CE⊥AD,垂足为E.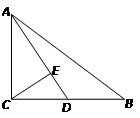
求:(1)线段CD的长;
(2)cos∠DCE的值.
(1)4
(2)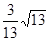
解析考点:解直角三角形.
分析:(1)在直角△ABC中,根据∠B的正弦即可求得AC,根据勾股定理即可求得BC,进而得到CD的长;
(2)∠DCE=∠CAD,只要在直角△ACD中求出∠CAD的余弦值即可.
解答:解:(1)在Rt△ABC中,∵∠C=90°,AC=6,sinB=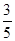 ,
,
∴AB=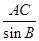 =6×
=6× =10.
=10.
BC=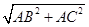 =
=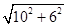 =8.
=8.
CD=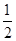 BC=4;
BC=4;
(2)在Rt△ACD中,∵CE⊥AD,
∴∠CAD=90°-∠ACE=∠DCE.(6分)
AD=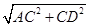 =
= =2
=2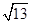 .
.
∴cos∠DCE=cos∠CAD=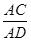 =
=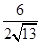 =
=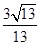 .
.
点评:在锐角的三角函数中,已知其中的一个就可求出另外几个,并且三角函数值的大小只与角的大小有关,而与所在三角形无关.

练习册系列答案
相关题目

 图象与x轴交点坐标;
图象与x轴交点坐标; 的两条高
的两条高 相交于点
相交于点 ,且
,且
 的角平分线上,并说明理由.
的角平分线上,并说明理由.
 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数图象.
(小时)之间的函数图象.
 小时,求乙车离出发地的距离
小时,求乙车离出发地的距离