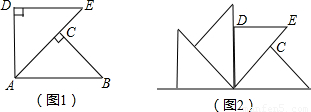题目内容
如图1中△ABC和△ADE都是等腰直角三角形,∠ACB=∠D=90°,点C在AE上,△ABC绕着A点沿逆时针旋转x度后能够与△ADE重合.若将图1作为“基本图形”绕着A点沿逆时针连续旋转y度可得到图2,则x、y的值分别为
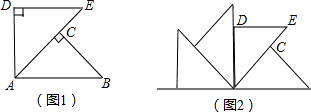
- A.90°,45°
- B.45°,90°
- C.60°,30°
- D.30°,60°
B
分析:先由等腰三角形的性质得到∠CAB和∠DAE的度数,再利用旋转的性质可分别求出x,y的值.
解答:∵△ABC和△ADE都是等腰直角三角形
∴∠CAB=∠DAE=45°
又∵△ABC绕着A点沿逆时针旋转x度后能够与△ADE重合
∴旋转中心为A点,旋转角度为45°,即x=45°
若把图1作为“基本图形”绕着A点沿逆时针连续旋转y度可得到图2
则y=45°+45°=90°
故选B.
点评:熟练掌握等腰三角形和旋转的性质.对于旋转要确定旋转中心,旋转方向以及旋转角度的大小.
分析:先由等腰三角形的性质得到∠CAB和∠DAE的度数,再利用旋转的性质可分别求出x,y的值.
解答:∵△ABC和△ADE都是等腰直角三角形
∴∠CAB=∠DAE=45°
又∵△ABC绕着A点沿逆时针旋转x度后能够与△ADE重合
∴旋转中心为A点,旋转角度为45°,即x=45°
若把图1作为“基本图形”绕着A点沿逆时针连续旋转y度可得到图2
则y=45°+45°=90°
故选B.
点评:熟练掌握等腰三角形和旋转的性质.对于旋转要确定旋转中心,旋转方向以及旋转角度的大小.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 24、如图,在△ABC和△DCB中AC与BD相交于点O,AB=DC.
24、如图,在△ABC和△DCB中AC与BD相交于点O,AB=DC.
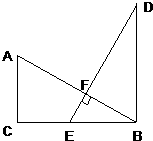 22、已知,如图,在△ABC和△EDB中,∠ACB=∠EBD=90°,点E在BC上,DE⊥AB交AB于F,且AB=ED.求证:DB=BC.
22、已知,如图,在△ABC和△EDB中,∠ACB=∠EBD=90°,点E在BC上,DE⊥AB交AB于F,且AB=ED.求证:DB=BC.