Question

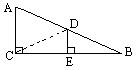
如图所示，某旅游地有一观景点A，此观景点建在一立石的顶端．为了方便游客，计划从地面B处向观景点A修建一座斜桥，今测得AC＝5m，BC＝12m，∠ACB＝．请推算：

(1)这座桥的长度是多少？

(2)为了使桥坚实稳固，计划在BC的中点处建一竖直立柱，以支撑桥面．这根立柱应建多高？

Answer 1

答案：
解析：

解(1)在Rt△ABC中 　　AB2＝BC2＋AC2＝122＋52＝169． 　　所以AB＝13m，即桥长为13m． 　　(2)如图，作线段BC的垂直平分线DE，交AB于D，交BC于E．则DE的长即为立柱的高．连接DC， 　　因为DE是线段BC的垂直平分线， 　　所以DB＝DC， 　　由此又得∠B＝∠DCB． 　　因为∠A和∠DCA分别为∠B和∠DCB的余角， 　　所以∠A＝∠DCA． 　　在△DCA中， 　　因为∠A＝∠DCA， 　　所以DC＝DA． 　　即　　DB＝DC＝DA＝AB． 　　在Rt△DBE中， 　　DB＝6.5m，BE＝6m． 　　DE2＝DB2－BE2＝6.52－62＝6.25． 　　所以DE＝2.5m，即立柱的高应为2.5m．

提示：

画出示意图，作线段BC的垂直平分线DE，交AB于D，交BC于E． 　　(1)根据勾股定理，由AC，BC的长可求得AB的长． 　　(2)连接DC，由线段的垂直平分线和等腰三角形的性质，先求得BD的长，再在Rt△DBE中，根据勾股定理求出DE的长．