题目内容
【题目】如图,四边形ABCD是菱形,∠A=60°,AB=6,扇形BEF的半径为6,圆心角为60°.
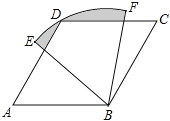
(1)连接DB,求证:∠DBF=∠ABE;
(2)求图中阴影部分的面积.
【答案】(1)见解析;(2)阴影部分的面积为60π﹣9![]() .
.
【解析】
(1)要证明∠DBF=∠ABE,需证∠EBF=ABD=60°,则∠ABE=∠DBF=60°﹣∠DBE,可得∠DBF=∠ABE;
(2)过B作BQ⊥DC于Q,则∠BQC=90°,可证明△ABM≌△DBN,阴影部分的面积S=S扇形DBC﹣S△DBC=![]() =60π﹣9
=60π﹣9![]() .
.
(1)证明:
∵四边形ABCD是菱形,
∴AD=AB,AD∥BC,
∵∠A=60°,
∴∠ADB=∠DBC=180°﹣60°﹣60°=60°,
即∠EBF=ABD=60°,
∴∠ABE=∠DBF=60°﹣∠DBE,
即∠DBF=∠ABE;
(2)解:过B作BQ⊥DC于Q,则∠BQC=90°,
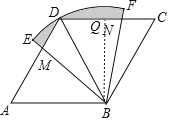
∵四边形ABCD是菱形,∠A=60°,AB=6,
∴DC∥AB,∠C=∠A=60°,BC=AB=6,
∴∠ADC=120°,
∴∠QBC=30°,
∴CQ=![]() BC=3,BQ=
BC=3,BQ=![]() CQ=3
CQ=3![]() ,
,
∵∠A=60°,∠CDB=120°﹣60°=60°,
∴∠A=∠CDB,
∵AB=BD,
∴在△ABM和△DBN中
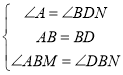
∴△ABM≌△DBN(ASA),
∴S△ABM=S△DBN,
∴阴影部分的面积S=S扇形DBC﹣S△DBC=![]() =60π﹣9
=60π﹣9![]() .
.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目