题目内容
某军舰以20节的速度由西向东航行，一艘电子侦察船以30节的速度由南向北航行，它能侦察出周围50海里（包括50海里）范围内的目标．如图，当该军舰行至A处时，电子侦察船正位于A处正南方向的B处，且AB=90海里，如果军船和侦察船仍按原速度沿原方向继续航行，那么航行途中侦察船能否侦察到这艘军舰？如果能，最早何时能侦察到？如果不能，请说明理由．
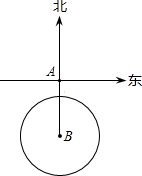
能．设侦察船最早由B出发经过x小时侦察到军舰，
则
≤50，
两边平方得：（90-30x）2+（20x）2≤502，
整理得13x2-54x+56≤0，
即（13x-28）（x-2）≤0，
∴2≤x≤
，
即当经过2小时至
小时时，侦察船能侦察到这艘军舰．
∴最早再过2小时能侦察到．
则
| (90-30x)2+(20x)2 |
两边平方得：（90-30x）2+（20x）2≤502，
整理得13x2-54x+56≤0，
即（13x-28）（x-2）≤0，
∴2≤x≤
| 28 |
| 13 |
即当经过2小时至
| 28 |
| 13 |
∴最早再过2小时能侦察到．
练习册系列答案
相关题目
