题目内容
一个质地均匀的正方形骰子的六个面上分别有1到6的点数，将骰子抛掷两次，抛第一次将朝上一面的点数记为x．抛第二次，将朝上一面的点数记为y，则点（x，y）落在直线y=-2x+8上的概率为（ ）
A．
| B．
| C．
| D．
|
根据题意画出树状图如下：
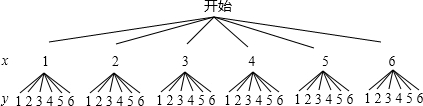
一共有36种情况，
x=1时，y=-2×1+8=6，
x=2时，y=-2×2+8=4，
x=3时，y=-2×3+8=2，
x=4时，y=-2×4+8=0（不符合题意，舍去），
在直线y=-2x+8上的点共有3个，
所以，P（A）=
=
．
故选B．
一共有36种情况，
x=1时，y=-2×1+8=6，
x=2时，y=-2×2+8=4，
x=3时，y=-2×3+8=2，
x=4时，y=-2×4+8=0（不符合题意，舍去），
在直线y=-2x+8上的点共有3个，
所以，P（A）=
| 3 |
| 36 |
| 1 |
| 12 |
故选B．
练习册系列答案
相关题目
任取两张卡片．