Question

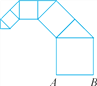
【题目】按如图所示的方式作正方形和等腰直角三角形．若第一个正方形的边长AB＝1，第一个正方形与第一个等腰直角三角形的面积和为S1，第二个正方形与第二个等腰直角三角形的面积和为S2……则第n个正方形与第n个等腰直角三角形的面积和Sn＝____．

Answer 1

【答案】

【解析】观察图形，根据正方形的四条边相等和等腰直角三角形的腰长为斜边长的倍，分别求得每个正方形的边长，从而发现规律，再根据规律求出第n个正方形与第n个等腰直角三角形的面积和即可．

解：∵第一个正方形的边长为1，

第2个正方形的边长为（）1=，

第3个正方形的边长为（）2=，

…，

第n个正方形的边长为（）n﹣1，

∴第n个正方形的面积为：[（）2]n﹣1=，

则第n个等腰直角三角形的面积为：×=，

故第n个正方形与第n个等腰直角三角形的面积和Sn=+=．

故答案为：．