题目内容
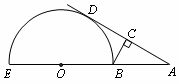
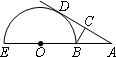
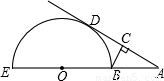
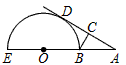
如图，EB为半圆O的直径，点A在EB的延长线上，AD切半圆O于点D，BC⊥AD，垂足为C，若AB=2cm，半圆O的半径为2cm，则BC的长为________cm．
1
分析：连接OD．根据切线的性质，得OD⊥AD．根据已知条件，得OA=2OD，从而得到∠A=30°，在直角三角形ABC中，根据30°所对的直角边是斜边的一半即可求解．
解答：
解：连接OD．
∵AD切半圆O于点D，
∴OD⊥AD．
∵AB=2cm，半圆O的半径为2cm，
∴OA=2OD，
∴∠A=30°，
∴BC=
AB=1（cm）．
故答案为1cm．
点评：此题综合运用了切线的性质和30°直角三角形的性质．
分析：连接OD．根据切线的性质，得OD⊥AD．根据已知条件，得OA=2OD，从而得到∠A=30°，在直角三角形ABC中，根据30°所对的直角边是斜边的一半即可求解．
解答：
解：连接OD．∵AD切半圆O于点D，
∴OD⊥AD．
∵AB=2cm，半圆O的半径为2cm，
∴OA=2OD，
∴∠A=30°，
∴BC=
AB=1（cm）．故答案为1cm．
点评：此题综合运用了切线的性质和30°直角三角形的性质．
练习册系列答案
相关题目
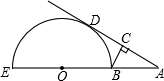如图，EB为半圆O的直径，点A在EB的延长线上，AD切半圆O于点D，BC⊥AD，垂足为C，若AB=2cm，半圆O的半径为2cm，则BC的长为
