Question

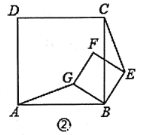
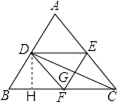
【题目】如图，△ABC中，∠ACB的平分线交AB于点D，作CD的垂直平分线，分别交AC、DC、BC于点E、G、F，连接DE、DF．

（1）求证：四边形DFCE是菱形；

（2）若∠ABC=60，∠ACB=45°，BD=2，试求BF的长．

Answer 1

【答案】（1）证明见解析；（2）1+

【解析】试题分析：（1）已知EF是DC的垂直平分线，可得DE=EC，DF=CF，∠EGC=∠FGC=90°，再由ASA证得△CGE≌△FCG，根据全等三角形的性质可得GE=GF，所以DE=EC=DF=CF，根据四条边都相等的四边形为菱形，即可判定四边形DFCE是菱形；（2）过D作DH⊥BC于H，根据30°直角三角形的性质求得BH=1；在Rt△DHB中，根据勾股定理求得DH的长，再判定△DHF是等腰直角三角形，即可得DH=FH=，即可求得BF的长．

试题解析：

（1）证明：∵EF是DC的垂直平分线，

∴DE=EC，DF=CF，∠EGC=∠FGC=90°，

∵CD平分∠ACB，

∴∠ECG=∠FCG，

∵CG=CG，

∴△CGE≌△FCG（ASA），

∴GE=GF，

∴DE=EC=DF=CF，

∴四边形DFCE是菱形；

（2）过D作DH⊥BC于H，则∠DHF=∠DHB=90°，

∵∠ABC=60°，

∴∠BDH=30°，

∴BH=BD=1，

在Rt△DHB中，DH==，

∵四边形DFCE是菱形，

∴DF∥AC，

∴∠DFB=∠ACB=45°，

∴△DHF是等腰直角三角形，

∴DH=FH=，

∴BF=BH+FH=1+．