题目内容
| |||||||||||
答案:
解析:
解析:
(1) |
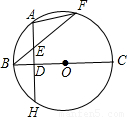
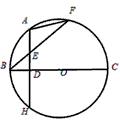
如图所示:连结FC,则BF⊥FC.
在△BDE和△BFC中,因为∠BFC=∠EDB= 解题指导:证明的是一个比例关系.一般可以利用相似三角形进行证明 |
(2) |
解:段BD与AE的大小关系是AE>BD.连结AC,AB,如图所示,则∠BAC=
解题指导:要比较两条线段的大小,通常应把这两条线段转移到一个三角形内,利用大角对大边来判断. |

练习册系列答案
相关题目



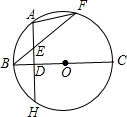 A是弧BF的中点,AH⊥BC.
A是弧BF的中点,AH⊥BC. A是弧BF的中点,AH⊥BC.
A是弧BF的中点,AH⊥BC.