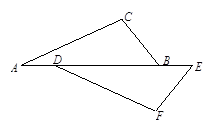题目内容
已知命题:如图,点A,D,B,E在同一条直线上,且AD=BE, ∠A=∠FDE,则△ABC≌△DEF.判断这个命题是真命题还是假命 题,如果是真命题,请给出证明;如果是假命题,请添加一个适当 条件使它成为真命题,并加以证明.

解:是假命题.
以下任一方法均可:
①添加条件:AC=DF.
证明:∵AD=BE,
∴AD+BD=BE+BD,即AB=DE.
在△ABC和△DEF中,
![]() AB=DE,
AB=DE,
∠A=∠FDE,
AC=DF,
∴△ABC≌△DEF(SAS).
②添加条件:∠CBA=∠E.
证明:∵AD=BE,
∴AD+BD=BE+BD,即AB=DE.
在△ABC和△DEF中,
![]() ∠A=∠FDE,
∠A=∠FDE,
AB=DE,
∠CBA=∠E ,
∴△ABC≌△DEF(ASA).
③添加条件:∠C=∠F.
证明:∵AD=BE,
∴AD+BD=BE+BD,即AB=DE.
在△ABC和△DEF中,
![]() ∠A=∠FDE,
∠A=∠FDE,
∠C=∠F ,
AB=DE, ∴△ABC≌△DEF(AAS)


练习册系列答案
相关题目
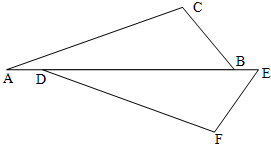 20、已知命题:如图,点A,D,B,E在同一条直线上,且AD=BE,∠A=∠FDE,则△ABC≌△DEF.判断这个命题是真命题还是假命题,如果是真命题,请给出证明;如果是假命题,请添加一个适当条件使它成为真命题,并加以证明.
20、已知命题:如图,点A,D,B,E在同一条直线上,且AD=BE,∠A=∠FDE,则△ABC≌△DEF.判断这个命题是真命题还是假命题,如果是真命题,请给出证明;如果是假命题,请添加一个适当条件使它成为真命题,并加以证明.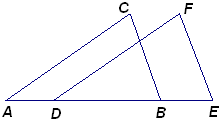 24、已知命题:“如图,点A、D、B、E在同一条直线上,且AD=BE,AC∥DF,则△ABC≌△DEF.”这个命题是真命题还是假命题?如果是真命题,请给出证明; 如果是假命题,请添加一个适当的条件,使它成为真命题,并加以证明.
24、已知命题:“如图,点A、D、B、E在同一条直线上,且AD=BE,AC∥DF,则△ABC≌△DEF.”这个命题是真命题还是假命题?如果是真命题,请给出证明; 如果是假命题,请添加一个适当的条件,使它成为真命题,并加以证明.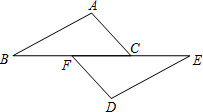 (2011•郑州模拟)已知命题:“如图,点B、F、C、E在同一条直线上,则AB∥DE.”判断这个命题是真命题还是假命题,如果是真命题,请给出证明;如果是假命题,在不添加其他辅助线的情况下,请添加一个适当的条件使它成为真命题,并加以证明.
(2011•郑州模拟)已知命题:“如图,点B、F、C、E在同一条直线上,则AB∥DE.”判断这个命题是真命题还是假命题,如果是真命题,请给出证明;如果是假命题,在不添加其他辅助线的情况下,请添加一个适当的条件使它成为真命题,并加以证明.