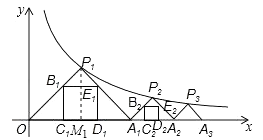
题目内容
【题目】在等腰三角形中,过其中的一个顶点的直线如果能把这个等腰三角形分成两个小的等腰三角形,我们称这种等腰三角形为“少见的三角形”,这条直线称为分割线,下面我们来研究这类三角形.
(1)等腰直角三角形是不是“少见的三角形”?
(2)已知如图所示的钝角三角形是一个“少见的三角形”,请你画出分割线的大致位置,并求出顶角的度数;
(3)锐角三角形中有没有“少见的三角形”?如果没有,请说明理由;如果有,请画出图形并求出顶角的度数.

【答案】(1)等腰直角三角形是“少见的三角形”;(2)顶角∠BAC=108°;画图见解析;(3)有,顶角是36°;画图见解析.
【解析】
(1)画出图形,利用三角形内角和进行计算,可得等腰直角三角形是“少见的三角形”;
(2)画出图形,利用等腰三角形的性质、三角形内角和进行解答;
(3)有,画出图形,利用等腰三角形的性质、三角形内角和进行解答.
解:(1)如图1,
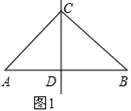
当过顶角∠C的顶点的直线CD把△ABC分成了两个等腰三角形,则AC=BC,AD=CD=BD,
设∠A=x°,
则∠ACD=∠A=x°,∠B=∠A=x°,
∴∠BCD=∠B=x°,
∵∠A+∠ACB+∠B=180°
∴x+x+x+x=180,
解得x=45,
则顶角是90°;
∴△ABC是等腰直角三角形,
即等腰直角三角形是“少见的三角形”;
(2)如图2,
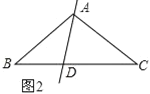
AC=CD=AB,BD=AD,
设∠B=x°,
∵AB=AC,
∴∠C=∠B=x°,
∵BD=AD,
∴∠BAD=∠B=x°,
∴∠ADC=∠B+∠BAD=2x°,
∵AC=DC,
∴∠ADC=∠CAD=2x°,
∴∠BAC=3x°,
∴x+x+3x=180,
x=36°,
则顶角∠BAC=108°.
(3)如图3,
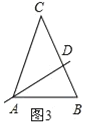
当过底角∠CAB的角平分线AD把△ABC分成了两个等腰三角形,则有AC=BC,AB=AD=CD,
设∠C=x°,
∵AD=CD,
∴∠CAD=∠C=x°,
∴∠ADB=∠CAD+∠C=2x°,
∵AD=AB,
∴∠B=∠ADB=2x°,
∵AC=BC,
∴∠CAB=∠B=2x°,
∵∠CAB+∠B+∠C=180°,
∴x+2x+2x=180,
x=36°,
则顶角是36°.