Question

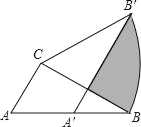
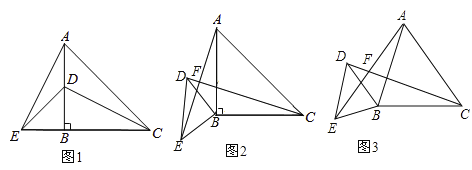
【题目】如图，在△ABC中，点D在边AB上，点F、E在边AC上，且DF∥BE，．

（1）求证：DE∥BC；

（2）如果，S△ADF=2，求S△ABC的值．

Answer 1

【答案】（1）证明见解析；（2）

【解析】

（1）由DF∥BE得比例，结合已知比例，利用过渡比得出，证明结论；

（2）△ADF与△DEF等高，根据等高的两个三角形面积比等于底边的比，求△DEF的面积，得出△ADE的面积，再由DE∥BC，得出△ADE∽△ABC，利用相似三角形的面积比等于相似比的平方求解．

（1）证明：∵DF∥BE，

∴

∵，

∴

∴DE∥BC．

（2）∵，

∴，

∴．

设△ADE中边AE上的高为h．

∴，

∴S△DEF＝×2＝3．

∴S△ADE=2+3=5．

∵DE∥BC，

∴△ADE∽△ABC．

∴．

∴S△ABC＝．