题目内容
(本题8分)如图,数轴上有三个点A、B、C,表示的数分别是-4、-2、3,请回答:
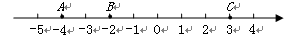
小题1:(1)若将点B向左移动5个单位后,三个点所表示的数中,最小的数是 ;
小题2:(2)若使C、B两点的距离与A、B两点的距离相等,则需将点C向左移动
个单位;
小题3:(3)若移动A、B、C三点中的两个点,使三个点表示的数相同,移动方法有 种,其中移动所走的距离和最大的是 个单位;
小题4:(4)若在原点处有一只小青蛙,一步跳1个单位长. 小青蛙第1次先向左跳1步,第2次再向右跳3步,然后第3次再向左跳5步,第4次再向右跳7步,…,按此规律继续跳下去,那么跳第100次时,应跳 步,落脚点表示的数是 ;跳了第n次(n是正整数)时,落脚点表示的数是 .
小题5:(5)数轴上有个动点表示的数是x,求|x-2︱+|x+3|的最小值.
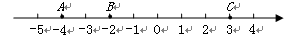
小题1:(1)若将点B向左移动5个单位后,三个点所表示的数中,最小的数是 ;
小题2:(2)若使C、B两点的距离与A、B两点的距离相等,则需将点C向左移动
个单位;
小题3:(3)若移动A、B、C三点中的两个点,使三个点表示的数相同,移动方法有 种,其中移动所走的距离和最大的是 个单位;
小题4:(4)若在原点处有一只小青蛙,一步跳1个单位长. 小青蛙第1次先向左跳1步,第2次再向右跳3步,然后第3次再向左跳5步,第4次再向右跳7步,…,按此规律继续跳下去,那么跳第100次时,应跳 步,落脚点表示的数是 ;跳了第n次(n是正整数)时,落脚点表示的数是 .
小题5:(5)数轴上有个动点表示的数是x,求|x-2︱+|x+3|的最小值.
小题1:-7
小题2:3或7
小题3:3 12
小题4:199 100 (-1)nn
小题5:5
分析:(1)根据图形,点B向左移动5个单位,则点B表示-7,然后根据数轴上的数右边的总比左边的大解答;
(2)先求出A、B两点的距离为2,然后使C到B的距离等于2即可;
(3)每固定一个点就是一种方法,所以共有三种,分别求出三种情况的距离之和,即可得解;
(4)根据规律发现,所列步数是奇数列,写出表达式,然后把n=100代入进行计算即可求解,根据向左跳是负数,向右跳是正数,列出算式,然后两个数一组就,计算后再求和即可,当跳了n次时,分n是偶数与n是奇数两种情况讨论求解;
(5)数轴上有个动点表示的数是x,|x-2︱+|x+3|的最小值是5。
解答:
(1)点B向左移动5个单位,表示的数是-7,根据图形,最小的数是-7;
(2)AB=(-2)-(-4)=-2+4=2,
设点C移动后表示的数是x,则|-2-x|=2,
∴x+2=2或x+2=-2,
解得x=0或x=-4,
当x=0时,3-0=3,
当x=-4时,3-(-4)=7,
∴点C向左移动3或7个单位;
(3)有①点A、B向点C移动,②点B、C向点A移动,③点A、C向点B移动,三种情况,
①移动距离为:7+5=12,
②移动距离为:2+7=9,
③移动距离为:2+5=7,
∴所走距离之和最大的是A、B向点C移动,为12;
∴移动方法有3种,最大距离之和为12;
(4)∵第1次跳1步,第2次跳3步,第3次跳5步,第4次跳7步,
…
∴第n次跳(2n-1)步,
当n=100时,2×100-1=200-1=199,
此时,所表示的数是:-1+3-5+7-…-197+199,
=(-1+3)+(-5+7)+…+(-197+199),
=2×100/2
=100。
①当n是偶数时,表示的数是:-1+3-5+7-…-(2n-3)+(2n-1),
=(-1+3)+(-5+7)+…+[-(2n-3)+(2n-1)],
=2×n /2
=n,
②当n是奇数时,表示的数是:-1+3-5+7-…-(2n-5)+(2n-3)-(2n-1),
=(-1+3)+(-5+7)+…+[-(2n-5)+(2n-3)]-(2n-1),
=2×(n-1)/2-(2n-1),
=n-1-2n+1,
=-n,
∴跳了第n次(n是正整数)时,落脚点表示的数是(-1)nn.
(5)|x-2|+|x+3|表示数轴上一点到2,-3和,当x为 0时和最小,最小距离是2和-3之间的距离是:2-(-3)=5。
点评:本题借助数轴考查了数轴上两点之间的距离的求解问题,以及数字变化规律的探讨问题,综合性较强,难度较大,但只要仔细分析,从中理清问题变化的思路便不难求解,此题计算求解时一定要仔细认真。

练习册系列答案
相关题目


 >
>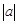
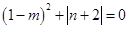 ,则
,则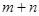 的值等于___________.
的值等于___________.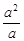 +a),(
+a),(