题目内容

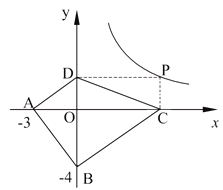
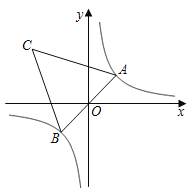
【题目】如图，在反比例函数的图象上有一动点，连接并延长交图象的另一支于点，在第二象限内有一点，满足，当点运动时，点始终在函数的图象上运动，若，则的值为（ ）

A.B.C.D.

【答案】A

【解析】

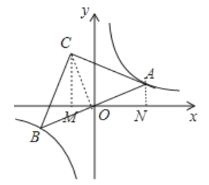
根据题意连接OC，作CM⊥x轴于M，AN⊥x轴于N，如图，利用反比例函数的性质得OA=OB，根据等腰三角形的性质得OC⊥AB，利用正切的定义得到，再证明Rt△OCM∽Rt△OAN，利用相似的性质得，然后根据k的几何意义即可求k的值．

解：连接OC，作CM⊥x轴于M，AN⊥x轴于N，如图，

∵A、B两点为反比例函数与正比例函数的两交点，

∴点A、点B关于原点对称，

∴OA=OB，

∵CA=CB，

∴OC⊥AB，

在Rt△AOC中，tan∠CAO=，

∵∠COM+∠AON=90°，∠AON+∠OAN=90°，

∴∠COM=∠OAN，

∴Rt△OCM∽Rt△OAN，

∴，

而，

∴S△CMO=6，

∵|k|=6，而k＜0，

∴k=-12．

故选：A．

练习册系列答案
相关题目

【题目】学以致用：问题1：怎样用长为的铁丝围成一个面积最大的矩形？

小学时我们就知道结论：围成正方形时面积最大，即围成边长为的正方形时面积最大为．请用你所学的二次函数的知识解释原因．

思考验证：问题2：怎样用铁丝围一个面积为且周长最小的矩形？

小明猜测：围成正方形时周长最小．

为了说明其中的道理，小明翻阅书籍，找到下面的结论：

在、均为正实数）中，若为定值，则，只有当时，有最小值．

思考验证：证明：、均为正实数）

请完成小明的证明过程：

证明：对于任意正实数、

　　

解决问题：

（1）若，则　　（当且仅当　　时取“” ；

（2）运用上述结论证明小明对问题2的猜测；

（3）填空：当时，的最小值为　　．

【题目】如图（1），已知点G在正方形ABCD的对角线AC上，GE⊥BC，垂足为点E，GF⊥CD，垂足为点F．

（1）证明与推断：

①求证：四边形CEGF是正方形；

②推断：的值为　 　：

（2）探究与证明：

将正方形CEGF绕点C顺时针方向旋转α角（0°＜α＜45°），如图（2）所示，试探究线段AG与BE之间的数量关系，并说明理由：

（3）拓展与运用：

正方形CEGF在旋转过程中，当B，E，F三点在一条直线上时，如图（3）所示，延长CG交AD于点H．若AG=6，GH=2，则BC=　 　．

【题目】在平面直角坐标系中，的半径为，点与圆心不重合，给出如下定义：若在上存在一点，使，则称点为的特征点．

（1）当的半径为1时，如图1．

①在点，，中，的特征点是__________．

②点在直线上，若点为的特征点，求的取值范围．

（2）如图2，的圆心在轴上，半径为2，点，．若线段上的所有点都是的特征点，直接写出圆心的横坐标的取值范围．

【题目】阅读理解：对于任意正实数a、b，∵≥0，　∴≥0，

∴≥，只有当a＝b时，等号成立．

结论：在≥（a、b均为正实数）中，若ab为定值p，则a+b≥，只有当a＝b时，a+b有最小值．

根据上述内容，回答下列问题：

若m＞0，只有当m＝ 时，有最小值 ．

思考验证：如图1，AB为半圆O的直径，C为半圆上任意一点（与点A、B不重合），过点C作CD⊥AB，垂足为D，AD＝a，DB＝b．

试根据图形验证≥，并指出等号成立时的条件．

探索应用：如图2，已知A(－3，0)，B(0，－4)，P为双曲线（x＞0）上的任意一点，过点P作PC⊥x轴于点C，PD⊥y轴于点D．求四边形ABCD面积的最小值，并说明此时四边形ABCD的形状．

【题目】太原双塔寺又名永祚寺，是国家级文物保护单位，由于双塔（舍利塔、文峰塔）耸立，被人们称为“文笔双塔”，是太原的标志性建筑之一，某校社会实践小组为了测量舍利塔的高度，在地面上的C处垂直于地面竖立了高度为2米的标杆CD，这时地面上的点E，标杆的顶端点D，舍利塔的塔尖点B正好在同一直线上，测得EC＝4米，将标杆CD向后平移到点C处，这时地面上的点F，标杆的顶端点H，舍利塔的塔尖点B正好在同一直线上（点F，点G，点E，点C与塔底处的点A在同一直线上），这时测得FG＝6米，GC＝53米．

请你根据以上数据，计算舍利塔的高度AB．

【题目】如图1，抛物线y＝x2+（m﹣2）x﹣2m（m＞0）与x轴交于A、B两点（A在B左边），与y轴交于点C．连接AC、BC，D为抛物线上一动点（D在B、C两点之间），OD交BC于E点．

（1）若△ABC的面积为8，求m的值；

（2）在（1）的条件下，求的最大值；

（3）如图2，直线y＝kx+b与抛物线交于M、N两点（M不与A重合，M在N左边），连MA，作NH⊥x轴于H，过点H作HP∥MA交y轴于点P，PH交MN于点Q，求点Q的横坐标．

【题目】每年的月日为世界环保日，为了提倡低碳环保，某公司决定购买台节省能源的新设备，现有甲、乙两种型号的设备可供选购.经调查：购买台甲型设备比购买台乙型设备多花万元，购买台甲型设备比购买台乙型设备少花万元.

（1）求甲、乙两种型号设备每台的价格；

（2）该公司经决定购买甲型设备不少于台，预算购买节省能源的新设备资金不超过万元，你认为该公司有哪几种购买方案；

（3）在（2）的条件下，已知甲型设备每月的产量为吨，乙型设备每月的产量为吨.若每月要求产量不低于吨，为了节约资金，请你为该公司设计一种最省钱的购买方案.

【题目】黄石市在创建国家级文明卫生城市中，绿化档次不断提升．某校计划购进A，B两种树木共100棵进行校园绿化升级，经市场调查：购买A种树木2棵，B种树木5棵，共需600元；购买A种树木3棵，B种树木1棵，共需380元．

（1）求A种，B种树木每棵各多少元？

（2）因布局需要，购买A种树木的数量不少于B种树木数量的3倍．学校与中标公司签订的合同中规定：在市场价格不变的情况下（不考虑其他因素），实际付款总金额按市场价九折优惠，请设计一种购买树木的方案，使实际所花费用最省，并求出最省的费用．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网