题目内容
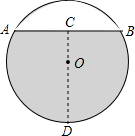 如图所示是一个水平放置的圆柱形水管的横截面,已知水平面高CD和水面宽AB均为80cm,则水管横截面圆的半径为
如图所示是一个水平放置的圆柱形水管的横截面,已知水平面高CD和水面宽AB均为80cm,则水管横截面圆的半径为50
50
cm.分析:先根据垂径定理得出BC的长,再设OB=x,则OC=80-x,在Rt△OBC中利用勾股定理即可求出OB的值.
解答:解:∵CD⊥AB,AB的长为40cm,
∴AC=BC=
AB=
×80=40cm,
设OB=x,则OC=80-x,
在Rt△OBC中,
OB2=OC2+BC2,即x2=(80-x)2+402,
解得x=40,即OB=50cm.
故答案为:50.
∴AC=BC=
| 1 |
| 2 |
| 1 |
| 2 |
设OB=x,则OC=80-x,
在Rt△OBC中,
OB2=OC2+BC2,即x2=(80-x)2+402,
解得x=40,即OB=50cm.
故答案为:50.
点评:本题考查的是垂径定理的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
 5、如图所示为一水平放置的转盘,使劲转动其指针,并让它自由停下,下面叙述正确的是( )
5、如图所示为一水平放置的转盘,使劲转动其指针,并让它自由停下,下面叙述正确的是( )