题目内容
先阅读以下材料,然后解答问题:
材料:将二次函数y=-x2+2x+3的图象向左平移1个单位,再向下平移2个单位,求平移后的抛物线的解析式(平移后抛物线的形状不变).
在抛物线y=-x2+2x+3图象上任取两点A(0,3)、B(1,4),由题意知:点A向左平移1个单位得到A′(-1,3),再向下平移2个单位得到A″(-1,1);点B向左平移1个单位得到B′(0,4),再向下平移2个单位得到B″(0,2).
设平移后的抛物线的解析式为y=-x2+bx+c.则点A″(-1,1),B″(0,2)在抛物线上.可得:
,解得:
.所以平移后的抛物线的解析式为:y=-x2+2.
根据以上信息解答下列问题:
将直线y=2x-3向右平移3个单位,再向上平移1个单位,求平移后的直线的解析式.
材料:将二次函数y=-x2+2x+3的图象向左平移1个单位,再向下平移2个单位,求平移后的抛物线的解析式(平移后抛物线的形状不变).
在抛物线y=-x2+2x+3图象上任取两点A(0,3)、B(1,4),由题意知:点A向左平移1个单位得到A′(-1,3),再向下平移2个单位得到A″(-1,1);点B向左平移1个单位得到B′(0,4),再向下平移2个单位得到B″(0,2).
设平移后的抛物线的解析式为y=-x2+bx+c.则点A″(-1,1),B″(0,2)在抛物线上.可得:
|
|
根据以上信息解答下列问题:
将直线y=2x-3向右平移3个单位,再向上平移1个单位,求平移后的直线的解析式.
在直线y=2x-3上任取一点A(0,-3),由题意知A向右平移3个单位,再向上平移1个单位得到A′(3,-2),
设平移后的解析式为y=2x+b,
则A′(3,-2)在y=2x+b的解析式上,
-2=2×3+b,
解得:b=-8,
所以平移后的直线的解析式为y=2x-8.
设平移后的解析式为y=2x+b,
则A′(3,-2)在y=2x+b的解析式上,
-2=2×3+b,
解得:b=-8,
所以平移后的直线的解析式为y=2x-8.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
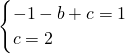 ,解得:
,解得: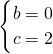 .所以平移后的抛物线的解析式为:y=-x2+2.
.所以平移后的抛物线的解析式为:y=-x2+2.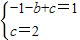 ,解得:
,解得: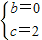 .所以平移后的抛物线的解析式为:y=-x2+2.
.所以平移后的抛物线的解析式为:y=-x2+2. 的图象向左平移1个单位,再向下平移2个单位,求平移后的抛物线的解析式(平移后抛物线的形状不变)。
的图象向左平移1个单位,再向下平移2个单位,求平移后的抛物线的解析式(平移后抛物线的形状不变)。 (
( ,3),再向下平移2个单位得到
,3),再向下平移2个单位得到 (
( (0,4),再向下平移2个单位得到
(0,4),再向下平移2个单位得到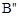 (0,2)。
(0,2)。 。
。 ,解得:
,解得: 。
。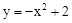 。
。 向右平移3个单位,再向上平移1个单位,求平移后的直线的解析式。
向右平移3个单位,再向上平移1个单位,求平移后的直线的解析式。