题目内容
(2008•衡阳)如图1,在平面直角坐标系中,等边三角形ABC的两顶点坐标分别为A(1,0),B(2,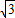 ),CD为△ABC的中线,⊙M与△ACD的外接圆,BC交⊙M于点N.
),CD为△ABC的中线,⊙M与△ACD的外接圆,BC交⊙M于点N.(1)将直线AB绕点D顺时针旋转使得到的直线l与⊙M相切,求此时的旋转角及直线l的解析式;
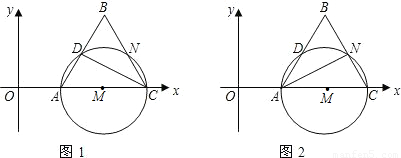
(2)连接MN,试判断MN与CD是否互相垂直平分,并说明理由;
(3)在(1)中的直线l上是否存在点P,使△PAN为直角三角形?若存在,求出所有满足条件的点P的坐标;若不存在,请说明理由.(图2为备用图)
【答案】分析:(1)相切时∠MDA=90°,原来是60°,所以应是逆时针旋转了30°,根据CD⊥等边三角形的一边,可得点D的纵坐标应是点B的纵坐标的一半;横坐标应是点A的横坐标加上A,B横坐标之差的一半.逆时针旋转30°后,可设直线与x的交点为P,那么PA=AD=1,则P(0,0),设出正比例函数解析式,把点D的坐标代入即可求得解析式;
(2)易得∠ANC=90°,那么AN=NC,AM=MC,可得MN∥AB,那么MN⊥CD,易得△MNC是等边三角形,利用得到的垂直,那么可利用全等证得MN被CD平分,继而推出所求结论;
(3)△PAN为直角三角形,那么有可能点P是直角顶点,还有可能是点A是直角顶点及点N的直角顶点.应分三种情况探讨.注意使用特殊的三角函数和勾股定理求解.
解答: 解:(1)连接MD,则∠MDA=60度,当AB绕点D,顺时针旋转使得到的直线l与圆M相切时,DM⊥AB,∠MDA=90度,所以,此时的旋转角是顺时针30度.未旋转时,点D坐标(1.5,
解:(1)连接MD,则∠MDA=60度,当AB绕点D,顺时针旋转使得到的直线l与圆M相切时,DM⊥AB,∠MDA=90度,所以,此时的旋转角是顺时针30度.未旋转时,点D坐标(1.5,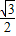 ),可设直线与x的交点为P,那么PA=AD=1,则P(0,0),设出正比例函数解析式为y=kx,过点D,所以l的解析式为:y=
),可设直线与x的交点为P,那么PA=AD=1,则P(0,0),设出正比例函数解析式为y=kx,过点D,所以l的解析式为:y=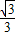 x;
x;
(2)MN⊥CD,且与CD互相垂直平分,因为点N是BC的中点,MN是中位线,有CD⊥AB,MN∥AB,所以MN⊥CD,同时MN平分CD,同时利用MN连线与CD的交点及点C组成的两个三角形全等,得出CD也平分了MN;
(3)第1种情况:PA⊥AN,P( ,
,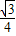 );
);
第2种情况:PN⊥AN,P( ,
,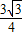 );
);
第3种情况:PA⊥PN,以AN为直径的圆与直线l的交点有2个,
AN=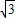 ,
,
设直线l上的点P坐标为(x,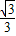 x),则PA2+PN2=AN2=3,
x),则PA2+PN2=AN2=3,
N点坐标为( ,
,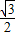 ),
),
(x-1)2+( x)2+(x-
x)2+(x- )2+(
)2+(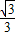 x-
x-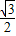 )2=3,
)2=3,
解得x=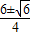 ,这是P点的横坐标,
,这是P点的横坐标,
∴P点纵坐标是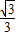 x.
x.
点评:求直线解析式,应得到相应的两个点的坐标;有2个以上中点时,应考虑使用三角形的中位线定理.
(2)易得∠ANC=90°,那么AN=NC,AM=MC,可得MN∥AB,那么MN⊥CD,易得△MNC是等边三角形,利用得到的垂直,那么可利用全等证得MN被CD平分,继而推出所求结论;
(3)△PAN为直角三角形,那么有可能点P是直角顶点,还有可能是点A是直角顶点及点N的直角顶点.应分三种情况探讨.注意使用特殊的三角函数和勾股定理求解.
解答:
 解:(1)连接MD,则∠MDA=60度,当AB绕点D,顺时针旋转使得到的直线l与圆M相切时,DM⊥AB,∠MDA=90度,所以,此时的旋转角是顺时针30度.未旋转时,点D坐标(1.5,
解:(1)连接MD,则∠MDA=60度,当AB绕点D,顺时针旋转使得到的直线l与圆M相切时,DM⊥AB,∠MDA=90度,所以,此时的旋转角是顺时针30度.未旋转时,点D坐标(1.5,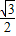 ),可设直线与x的交点为P,那么PA=AD=1,则P(0,0),设出正比例函数解析式为y=kx,过点D,所以l的解析式为:y=
),可设直线与x的交点为P,那么PA=AD=1,则P(0,0),设出正比例函数解析式为y=kx,过点D,所以l的解析式为:y=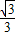 x;
x;(2)MN⊥CD,且与CD互相垂直平分,因为点N是BC的中点,MN是中位线,有CD⊥AB,MN∥AB,所以MN⊥CD,同时MN平分CD,同时利用MN连线与CD的交点及点C组成的两个三角形全等,得出CD也平分了MN;
(3)第1种情况:PA⊥AN,P(
 ,
,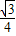 );
);第2种情况:PN⊥AN,P(
 ,
,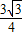 );
);第3种情况:PA⊥PN,以AN为直径的圆与直线l的交点有2个,
AN=
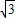 ,
,设直线l上的点P坐标为(x,
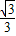 x),则PA2+PN2=AN2=3,
x),则PA2+PN2=AN2=3,N点坐标为(
 ,
,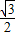 ),
),(x-1)2+(
 x)2+(x-
x)2+(x- )2+(
)2+(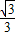 x-
x-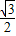 )2=3,
)2=3,解得x=
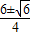 ,这是P点的横坐标,
,这是P点的横坐标,∴P点纵坐标是
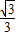 x.
x.点评:求直线解析式,应得到相应的两个点的坐标;有2个以上中点时,应考虑使用三角形的中位线定理.

练习册系列答案
相关题目