题目内容
抛物线 与
与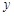 轴交于
轴交于 点.
点.
(1)求出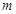 的值并画出这条抛物线;
的值并画出这条抛物线;
(2)求它与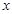 轴的交点和抛物线顶点的坐标;
轴的交点和抛物线顶点的坐标;
(3)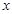 取什么值时,抛物线在
取什么值时,抛物线在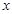 轴上方?
轴上方?
(4)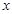 取什么值时,
取什么值时,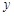 的值随
的值随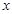 值增大而减小?
值增大而减小?
【答案】
(1)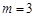 ;(2)
;(2)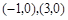 ,
,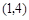 ;(3)
;(3)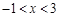 ;(4)
;(4)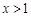
【解析】
试题分析:(1)把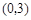 直接代入抛物线
直接代入抛物线 即得求得
即得求得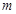 的值,再根据描点法作出图象;
的值,再根据描点法作出图象;
(2)根据与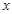 轴的交点的纵坐标为0,即可求出它与
轴的交点的纵坐标为0,即可求出它与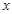 轴的交点,再把函数解析式配方为顶点式,即可求出顶点的坐标;
轴的交点,再把函数解析式配方为顶点式,即可求出顶点的坐标;
(3)根据抛物线在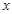 轴上方的部分的函数值大于0,即可得到结果;
轴上方的部分的函数值大于0,即可得到结果;
(4)根据函数的增减性即可得到结果。
(1)由抛物线 与
与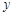 轴交于
轴交于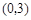 ,得:
,得: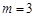 .
.
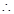 抛物线为
抛物线为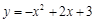 .图象略.
.图象略.
(2)由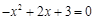 ,得
,得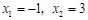 ,
,
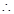 抛物线与
抛物线与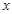 轴的交点为
轴的交点为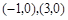 ;
;
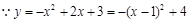 ,
,
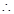 抛物线顶点坐标为
抛物线顶点坐标为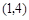 ;
;
(3)由图象可知:当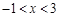 时,抛物线在
时,抛物线在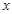 轴上方;
轴上方;
(4)由图象可知:当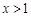 时,
时,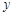 的值随
的值随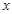 值的增大而减小.
值的增大而减小.
考点:本题考查的是二次函数的性质
点评:解答本题的关键是掌握函数图象上的点适合这个函数的解析式,图象与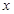 轴交点的坐标的纵坐标为0。
轴交点的坐标的纵坐标为0。

练习册系列答案
相关题目
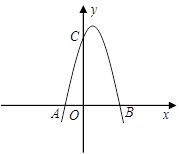
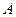 为顶点的抛物线与
为顶点的抛物线与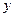 轴交于点
轴交于点 .已知
.已知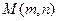 是抛物线上的一点(
是抛物线上的一点(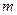 、
、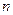 为正整数),且它位于对称轴的右侧.若以
为正整数),且它位于对称轴的右侧.若以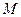 、
、 、
、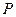 ,
, 是否总成立?请说明理由.
是否总成立?请说明理由.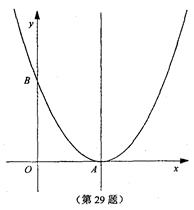
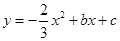 与
与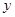 轴交于点
轴交于点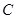 ,与
,与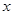 轴交与A、B两点(点A在点B的左侧),且OA=1,OC=2
轴交与A、B两点(点A在点B的左侧),且OA=1,OC=2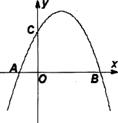
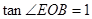 ,求点E的坐标;
,求点E的坐标; 为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由。
为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由。