题目内容
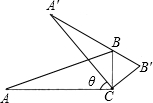某学生想把放置在水平桌面上的一块三角板ABC（∠ACB=90°，∠A=30°），绕点C按顺时针方向旋转θ角，转到△A′B′C的位置，其中A′，B′分别是A，B的对应点，B在A′B′上（如图所示），则θ角的度数为（ ）| A、30° | B、45° | C、60° | D、90° |
分析：根据题意有∠ACB=90°，∠A=30°，进而可得∠ABC=60°，又有∠ACA′=BCB′=∠ABA′=θ，可得∠CBB′=
（180°-θ），代入数据可得答案．
| 1 |
| 2 |
解答：解：∵∠ACB=90°，∠A=30°，
∴∠ABC=60°，
∴∠ACA′=BCB′=∠ABA′=θ，∠CBB′=
（180°-θ），
∴θ=∠ABC=60°．故选C．
∴∠ABC=60°，
∴∠ACA′=BCB′=∠ABA′=θ，∠CBB′=
| 1 |
| 2 |
∴θ=∠ABC=60°．故选C．
点评：本题考查旋转的性质：旋转变化前后，对应点到旋转中心的距离相等以及每一对对应点与旋转中心连线所构成的旋转角相等．要注意旋转的三要素：①定点是旋转中心；②旋转方向；③旋转角度．
练习册系列答案
相关题目
某学生想把放置在水平桌面上的一块三角板ABC（∠ACB=90°，∠A=30°），绕点C按顺时针方向旋转θ角，转到△A′B′C的位置，其中A′，B′分别是A，B的对应点，B在A′B′上（如图所示），则θ角的度数为