Question

梯形的两底角之和为90°，上底长为5，下底长为11，则连接两底中点的线段长是

1. A.
   3
2. B.
   4
3. C.
   5
4. D.
   6

Answer 1

A
分析：做EM∥AB，EN∥CD，分别交BC于M、N，根据平行四边形的判定可得到四边形AEMB是平行四边形，四边形EDCN是平行四边形，再根据平行四边形的性质可推出AE=BM，ED=NC，利用直角三角形斜边上的中线定理可判定△EMN为直角三角形，再根据线段之间的关系可推出F点为线段MN的中点，从而不难推出EF与BC-AD之间的数量关系，已知EF的长，则不难求解．
解答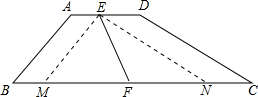：解：如图梯形ABCD，AD∥BC，∠B+∠C=90°，AD=5，BC=11，E，F分别是AD，BC的中点．
作EM∥AB，EN∥CD，分别交BC于M、N．
∵EM∥AB，EN∥CD，
∴∠B=∠EMN，∠C=∠ENM，
∵AD∥BC，
∴四边形AEMB是平行四边形，四边形EDCN是平行四边形，
∴AE=BM，ED=NC，
∵∠B+∠C=90°．
∴∠EMN+∠ENM=90°，
∴△EMN为直角三角形，
∵BF=FC，BM=AE，NC=ED，AE=ED，
∴BM=NC，
∴MF=FN，
∴F点为线段MN的中点，
∵△MEN为直角三角形，
∴EF=MN，
∵MN=BC-BM-NC=BC-AE-ED=BC-（AE+ED）=BC-AD，
∴EF=（BC-AD），
∵AD=5，BC=11
∴EF=3，
故选A．
点评：此题主要考查平行四边形的判定与性质及直角三角形斜边上的中线的定理的综合运用．