题目内容
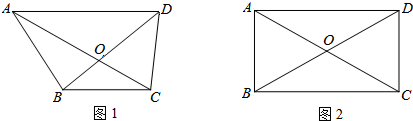
(2013•厦门质检)四边形ABCD中,对角线AC、BD的交点为O,
(1)如图1,若AD∥BC,AD=6,BC=4,求
的值;
(2)如图2,若四边形ABCD是矩形,过点B作BE⊥AC,垂足为E,当∠ACB=30°时,有AC=
BE+1,求BC的长度.
(1)如图1,若AD∥BC,AD=6,BC=4,求
| AO |
| CO |
(2)如图2,若四边形ABCD是矩形,过点B作BE⊥AC,垂足为E,当∠ACB=30°时,有AC=
| 3 |

分析:(1)先根据AD∥BC可知∠ACB=∠DAC,∠ADB=∠DBC,故可得出△AOD∽△COB,再根据相似三角形的对应边成比例即可得出结论;
(2)设BE=x,在Rt△BEC中,由∠ACB=30°可知BC=2BE=2x,在Rt△ABC中由cos∠ACB=
,可用x表示出AC的值,再根据AC=
BE+1可得出x的值,进而得出结论.
(2)设BE=x,在Rt△BEC中,由∠ACB=30°可知BC=2BE=2x,在Rt△ABC中由cos∠ACB=
| BC |
| AC |
| 3 |
解答: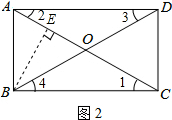 解:(1)∵AD∥BC,
解:(1)∵AD∥BC,
∴∠1=∠2,∠3=∠4,
∴△AOD∽△COB,
∴
=
=
=
;
(2)设BE=x,在Rt△BEC中,
∵∠ACB=30°,
∴BC=2BE=2x,
在Rt△ABC中,
∵cos∠ACB=
,
∴cos30°=
=
,
∴AC=
=
=
x,
又∵AC=
BE+1=
x+1,
∴
x=
x+1,解得x=
,
∴BC=2x=2
.
 解:(1)∵AD∥BC,
解:(1)∵AD∥BC,∴∠1=∠2,∠3=∠4,
∴△AOD∽△COB,
∴
| AO |
| CO |
| AD |
| BC |
| 6 |
| 4 |
| 3 |
| 2 |
(2)设BE=x,在Rt△BEC中,
∵∠ACB=30°,
∴BC=2BE=2x,
在Rt△ABC中,
∵cos∠ACB=
| BC |
| AC |
∴cos30°=
| 2x |
| AC |
| ||
| 2 |
∴AC=
| BC |
| cos30° |
| 4x | ||
|
4
| ||
| 3 |
又∵AC=
| 3 |
| 3 |
∴
4
| ||
| 3 |
| 3 |
| 3 |
∴BC=2x=2
| 3 |
点评:本题考查的是相似三角形的判定与性质,熟知相似三角形的判定与性质、锐角三角函数的定义及特殊角的三角函数值是解答此题的关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
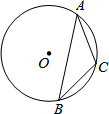 (2013•厦门质检)如图,A、B、C是⊙O上的三点,点C是劣弧AB的中点,∠A=40°,则∠B的度数等于( )
(2013•厦门质检)如图,A、B、C是⊙O上的三点,点C是劣弧AB的中点,∠A=40°,则∠B的度数等于( )