��Ŀ����
����Ŀ����ͼ��ʾ����ʦ�����������ڹ�·����ʻ��A��ʱ������B��A�ı�ƫ��60![]() �����ϣ���ʦ����ÿ����125���ٶ�����ʻ������C��ʱ������B��C�ı�ƫ��30
�����ϣ���ʦ����ÿ����125���ٶ�����ʻ������C��ʱ������B��C�ı�ƫ��30![]() �����ϣ�����D��ʱ������B��D�ı�ƫ��30
�����ϣ�����D��ʱ������B��D�ı�ƫ��30![]() �����ϣ�����������D��ʱǡ�����B���500�ף�
�����ϣ�����������D��ʱǡ�����B���500�ף�
(1)�жϡ�BCD����״��
(2)��������A������D������Ҫ��ʱ�䣺(3)��������A������ʻ6���ӵ���E��������ֱ��д����ʱ����B��E��ʲô�����ϣ�
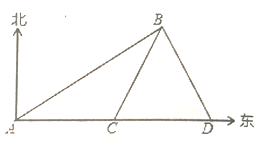
���𰸡�(1)��BCD�ǵȱ�������(2)������A������D������Ҫ��ʱ��Ϊ8����(3)����B��E������������
�������������������1����������ó���BCD=��BDC=60�������ɵó���BCD����״��
��2��������������ǵ������Լ��ȱ������ε����ʵó�AD�ij�����������𰸣�
��3�������������AE�ij��������õ��������ε����ʵó�B��E��λ�ù�ϵ��
����������⣺��1��������ɵã�
��4=��5=30��������BCD=��BDC=60��������BCD�ǵȱ������Σ�
��2���ߡ�BCD�ǵȱ������Σ�BD=500m����BC=CD=500m���ߡ�2=90�㩁��1=30�㣬��BCD=60�㣬���3=30�㣬��AC=BC=500m����AD=1000m����1000��125=8�����ӣ�����������A������D������Ҫ8���ӣ�
��3����������A������ʻ6���ӵ���E������AE=125��6=750��m������CE=250m����EΪCD���е㣬��BE��CD��������B��E����������


 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д� �㾦�½̲�ȫ�ܽ��ϵ�д�
�㾦�½̲�ȫ�ܽ��ϵ�д�