题目内容
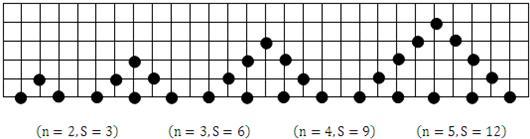
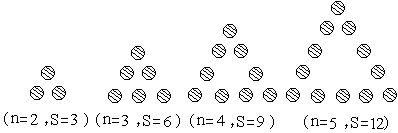
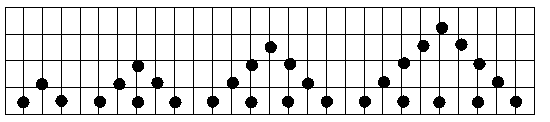
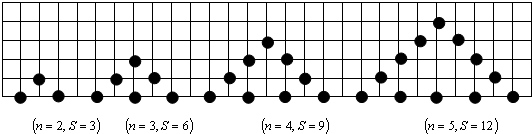
用棋子摆出下列一组三角形，三角形每边有n枚棋子，每个三角形的棋子总数为s，如图按此规律推断，当三角形的边上有n枚棋子时，该三角形棋子总数s=________（用含n的式子表示）．
3n-3
分析：观察不难发现，用每一条边上的棋子数乘以边数3，再减去三角形顶点处公共棋子，列式整理即可得解．
解答：n=2时，s=3×2-3=3，
n=3时，s=3×3-3=6，
n=4时，s=3×4-3=9，
n=5时，s=3×5-3=12，
…，
依此类推，三角形的边上有n枚棋子时，s=3n-3．
故答案为：s=3n-3．
点评：本题是对图形变化规律的考查，难点在于观察出三角形顶点处的棋子被两边公用．
分析：观察不难发现，用每一条边上的棋子数乘以边数3，再减去三角形顶点处公共棋子，列式整理即可得解．
解答：n=2时，s=3×2-3=3，
n=3时，s=3×3-3=6，
n=4时，s=3×4-3=9，
n=5时，s=3×5-3=12，
…，
依此类推，三角形的边上有n枚棋子时，s=3n-3．
故答案为：s=3n-3．
点评：本题是对图形变化规律的考查，难点在于观察出三角形顶点处的棋子被两边公用．
练习册系列答案
培优三好生系列答案
优化作业上海科技文献出版社系列答案
相关题目
