题目内容
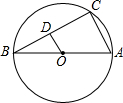AB是⊙O的直径，点C在⊙O上，OD∥AC，交BC于D．若BD=1，则BC的长为（ ）| A、2 | ||||
| B、3 | ||||
C、
| ||||
D、
|
分析：由AB为直径易知∠C=90°；因为OD∥AC，所以OD⊥BC，根据垂径定理得BC=2BD．
解答：解：∵AB是⊙O的直径，点C在⊙O上，
∴∠C=90°．
∵OD∥AC，
∴OD⊥BC．
∴BC=2BD=2．
故选A．
∴∠C=90°．
∵OD∥AC，
∴OD⊥BC．
∴BC=2BD=2．
故选A．
点评：此题考查了“直径所对的圆周角是直角”及垂径定理，属基础题．
练习册系列答案
导学全程练创优训练系列答案
相关题目
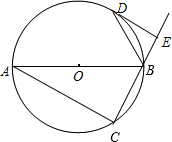
如图，AB是⊙O的直径，点D是
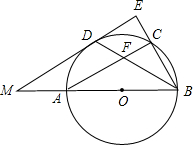
已知：如图，AB是⊙O的直径，点C在⊙O上，△ABC的外角平分线BD交⊙O于D，DE与⊙O相切，交CB的延长线于E．
（2013•淮北模拟）如图，已知AB是⊙O的直径，点C、D在⊙O上，且AB=10，AC=8．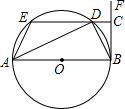
如图，AB是⊙O的直径，点C在⊙O的切线BF上，过C作直线CE⊥BF，交⊙O于点D、点E，连接AE、