题目内容
已知矩形纸片ABCD中,AB=4,BC=6.

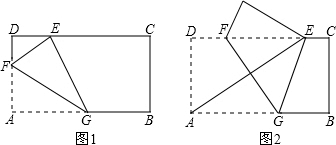
(1)如图1,点E是BC边上的一点,BE=2,AE、BD交于点F.①求AF:FE的值;②求△BEF的面积;
(2)如图2,将矩形纸片沿MN折叠,使点B与边CD的中点重合,点A、B的对应点为A1、B1,A1B1与DN交于点G,求△MCB1和△B1DG的周长之比.

(1)如图1,点E是BC边上的一点,BE=2,AE、BD交于点F.①求AF:FE的值;②求△BEF的面积;
(2)如图2,将矩形纸片沿MN折叠,使点B与边CD的中点重合,点A、B的对应点为A1、B1,A1B1与DN交于点G,求△MCB1和△B1DG的周长之比.
分析:(1)①由题意易证得△ADF∽△EBF,然后由相似三角形的对应边成比例,即可求得AF:FE的值;
②首先求得△ABD的面积,由等高三角形的面积比等于对应底的比,即可求得△ADF的面积,然后由相似三角形面积比等于相似比的平方,即可求得△BEF的面积;
(2)易证得△MCB1∽△B1DG,由勾股定理可求得CM的长,然后由相似三角形周长的比等于相似比,即可求得△MCB1和△B1DG的周长之比.
②首先求得△ABD的面积,由等高三角形的面积比等于对应底的比,即可求得△ADF的面积,然后由相似三角形面积比等于相似比的平方,即可求得△BEF的面积;
(2)易证得△MCB1∽△B1DG,由勾股定理可求得CM的长,然后由相似三角形周长的比等于相似比,即可求得△MCB1和△B1DG的周长之比.
解答:解:(1)①∵四边形ABCD是矩形,
∴AD∥BC,AD=BC=6,
∴△ADF∽△EBF,
∴AF:FE=AD:BE=6:2=3:1,
故AF:FE的值为3.
②∵△ADF∽△EBF,
∴DF:BF=AD:BE=3:1,
∴DF:BD=3:4,
∵S△ABD=
AB•AD=
×4×6=12,
∴S△ADF=
×S△ABD=9,
∵
=(
)2,
∴S△BEF=1;
(2)∵∠DGB1+∠DB1G=90°,∠DB1G+∠CB1M=90°,
∴∠DGB1=∠CB1M,
∵∠D=∠C=90°,
∴△MCB1∽△B1DG.
设CM=x,则B1M=BM=BC-CM=6-x,B1C=
DC=2,
∴x2+22=(6-x)2,
∴x=
,
∵△MCB1∽△B1DG,
∴
=
=
.
∴AD∥BC,AD=BC=6,
∴△ADF∽△EBF,
∴AF:FE=AD:BE=6:2=3:1,
故AF:FE的值为3.
②∵△ADF∽△EBF,
∴DF:BF=AD:BE=3:1,
∴DF:BD=3:4,
∵S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ADF=
| 3 |
| 4 |
∵
| S△ADF |
| S△BEF |
| AD |
| BE |
∴S△BEF=1;
(2)∵∠DGB1+∠DB1G=90°,∠DB1G+∠CB1M=90°,
∴∠DGB1=∠CB1M,
∵∠D=∠C=90°,
∴△MCB1∽△B1DG.
设CM=x,则B1M=BM=BC-CM=6-x,B1C=
| 1 |
| 2 |
∴x2+22=(6-x)2,
∴x=
| 8 |
| 3 |
∵△MCB1∽△B1DG,
∴
| C△MCB1 |
| C△B1DG |
| CM |
| B1D |
| 4 |
| 3 |
点评:此题考查了相似三角形的判定与性质、折叠的性质以及勾股定理.此题难度适中,注意掌握折叠前后图形的对应关系,注意掌握方程思想与数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
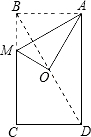 如图,已知矩形纸片ABCD中,AD=6,AB=a(a<6),在BC边上取一点M,将△ABM沿AM折叠后点B恰好落在矩形ABCD的对称中心O处,则a的值为
如图,已知矩形纸片ABCD中,AD=6,AB=a(a<6),在BC边上取一点M,将△ABM沿AM折叠后点B恰好落在矩形ABCD的对称中心O处,则a的值为