Question

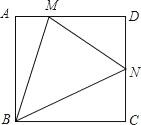
【题目】如图，在正方形ABCD中，N是DC上的点，且，M是AD上异于D的点，且∠NMB=∠MBC，则（　　）

A. B. C. D.

Answer 1

【答案】A

【解析】

从点B处作BF⊥MN交MN于点F，根据题意可设DN=3a，NC=4a，则CD=7a，首先证明△BFM≌△BAM推出AM=MF设AM=x，再证明△BCN≌△BFN，推出CN=NF，在Rt△DMN中利用勾股定理列出方程即可解决问题．

从点B处作BF⊥MN交MN于点F，

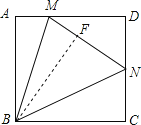
∵四边形ABCD是正方形，

∴AB=CD=AD，AD∥BC，∠A=∠C=∠D=90°，

∴∠AMB=∠MBC，

∵∠NMB=∠MBC，

∴∠BMA=∠BMF，

∵BA⊥MA，BF⊥MN，

∴AB=BF，

在Rt△BMA和Rt△BMF中，

，

∴Rt△BMA≌Rt△BMF，

∴AM=MF，

同理可证△BCN≌△BFN，

∴CN=NF，

设DN=3a，NC=4a，则CD=7a，则NF=4a，设AM=MF=x，

在Rt△DMN中，∵MN2=DM2+DN2

（3a）2+（7a-x）2=（4a+x）2，

解得x=，

∴AM=，

∵AB=CD=7a，

∴AM：AB=3：11；

故选A．