Question

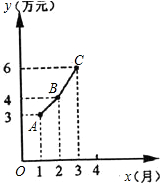
某公司2005年1-3月的月利润y（万元）与月份x之间的关系如图所示．图中的折线可近似看作是抛物线的一部分．
（1）根据图象提供的信息，求出过A、B、C三点的二次函数关系式；
（2）公司开展技术革新活动，定下目标：今年6月份的利润仍以图中抛物线的上升趋势上升．6月份公司预计将达到多少万元？
（3）如果公司1月份的利润率为13%，以后逐月增加1个百分点．已知6月上旬平均每日实际销售收入为3.6万元，照此推算6月份公司的利润是否会超过（2）中所确定的目标？
（成本总价=利润利润率，销售收入=成本总价+利润）

Answer 1

解：（1）设y与x之间的函数关系式为：
y=ax²+bx+c
依题意，得（）
解得a=，b=-，c=3
∴y与x之间的函数关系式为：y=x²-x+3

（2）当x=6时，解得y=18
∴预计6月份的利润将达到18万元

（3）6月份的利润率为：13%+5×1%=18%
6月份的实际销售收入为：3.6×30=108（万元）
解法一：设6月份的实际利润为x万元，依题意，得+x=108
解得x≈16.7（万元）
∵16.7万元＜18万元
∴6月份的利润不会达到原定目标
解法二：6月份预计销售收入：+18=118（万元）
∵108万元＜118万元
∴6月份的利润不会达到原定目标．
分析：（1）根据三点坐标易求解析式；
（2）即求当x=6时二次函数的值；
（3）因为6月份的利润目标已知，所以按增长速度求实际利润进行比较．
点评：前两个问题不难，最后一个问题有一个比较过程，选择利润比较直接，当然也可选择销售收入进行比较．