题目内容
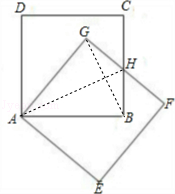
【题目】把正方形ABCD绕着点A,按顺时针方向旋转得到正方形AEFG,边FG与BC交于点H(如图).试问线段HG与线段HB相等吗?请先观察猜想,然后再证明你的猜想.

【答案】相等,证明见解析.
【解析】
试题分析:要证明HG与HB是否相等,可以把线段放在两个三角形中证明这两个三角形全等,或放在一个三角形中证明这个三角形是等腰三角形,而图中没有这样的三角形,因此需要作辅助线,构造三角形.
试题解析:HG=HB,
证法1:连接AH,
∵四边形ABCD,AEFG都是正方形,
∴∠B=∠G=90°,
由题意知AG=AB,又AH=AH,
∴Rt△AGH≌Rt△ABH(HL),
∴HG=HB.
证法2:连接GB,
∵四边形ABCD,AEFG都是正方形,
∴∠ABC=∠AGF=90°,
由题意知AB=AG,
∴∠AGB=∠ABG,
∴∠HGB=∠HBG,
∴HG=HB.
考点;1.正方形的性质;2.全等三角形的判定.

练习册系列答案
相关题目