题目内容
⊙O的半径为5,弦AB∥CD,AB=6,CD=8,则AB与CD距离为
- A.7
- B.8
- C.7或1
- D.1
C
分析:过O点作OE⊥AB,E为垂足,交CD与F,连OA,OC,由AB∥CD,得到OF⊥CD,根据垂径定理得AE=3,CF=4,再在Rt△OAE中和在Rt△OCF中分别利用勾股定理求出OE,OF,然后讨论:当圆O点在AB、CD之间,AB与CD之间的距离=OE+OF;当圆O点不在AB、CD之间,AB与CD之间的距离=OE-OF.
解答: 解:过O点作OE⊥AB,E为垂足,交CD与F,连OA,OC,如图,
解:过O点作OE⊥AB,E为垂足,交CD与F,连OA,OC,如图,
∵AB∥CD,
∴OF⊥CD,
∴AE=BE,CF=DF,
而AB=6,CD=8,
∴AE=3,CF=4,
在Rt△OAE中,OA=5,OE=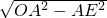 =
=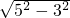 =4;
=4;
在Rt△OCF中,OC=5,OF= =
=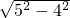 =3;
=3;
当圆O点在AB、CD之间,AB与CD之间的距离=OE+OF=7;
当圆O点不在AB、CD之间,AB与CD之间的距离=OE-OF=1;
所以AB与CD之间的距离为7或1.
故选C.
点评:本题考查了垂径定理,即垂直于弦的直径平分弦,并且平分弦所对的弧.也考查了勾股定理以及分类讨论的思想的运用.
分析:过O点作OE⊥AB,E为垂足,交CD与F,连OA,OC,由AB∥CD,得到OF⊥CD,根据垂径定理得AE=3,CF=4,再在Rt△OAE中和在Rt△OCF中分别利用勾股定理求出OE,OF,然后讨论:当圆O点在AB、CD之间,AB与CD之间的距离=OE+OF;当圆O点不在AB、CD之间,AB与CD之间的距离=OE-OF.
解答:
 解:过O点作OE⊥AB,E为垂足,交CD与F,连OA,OC,如图,
解:过O点作OE⊥AB,E为垂足,交CD与F,连OA,OC,如图,∵AB∥CD,
∴OF⊥CD,
∴AE=BE,CF=DF,
而AB=6,CD=8,
∴AE=3,CF=4,
在Rt△OAE中,OA=5,OE=
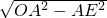 =
=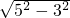 =4;
=4;在Rt△OCF中,OC=5,OF=
 =
=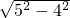 =3;
=3;当圆O点在AB、CD之间,AB与CD之间的距离=OE+OF=7;
当圆O点不在AB、CD之间,AB与CD之间的距离=OE-OF=1;
所以AB与CD之间的距离为7或1.
故选C.
点评:本题考查了垂径定理,即垂直于弦的直径平分弦,并且平分弦所对的弧.也考查了勾股定理以及分类讨论的思想的运用.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
⊙O的半径为5cm,弦AB∥CD,且AB=6cm,CD=8cm,则AB与CD之间的距离为( )
| A、1cm | B、7cm | C、3cm或4cm | D、1cm或7cm |
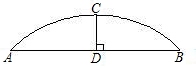 如图,一种花边是由弓形组成的,
如图,一种花边是由弓形组成的, |
| ACB |
| A、2 | ||
B、
| ||
| C、3 | ||
D、
|
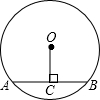 如图,⊙O的半径为5,弦AB=8,OC⊥AB于C,则OC的长等于
如图,⊙O的半径为5,弦AB=8,OC⊥AB于C,则OC的长等于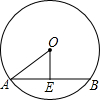 如图,⊙O的半径为2,弦AB=
如图,⊙O的半径为2,弦AB=