题目内容
(本题满分10分,其中每小题各5分)
在Rt△ABC中,∠ABC=90°,∠BAC=60°,D为BC中点,连结AD,过点D作DE⊥AD,交AB的延长线于E.

(1)若AD= ,求△ABC的面积;
,求△ABC的面积;
(2)求 的值.
的值.
(1)S△ABC=2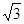 .(2)
.(2)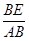 =
=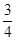 .
.
【解析】
试题分析:解:(1)∵∠ABC=90°,∠BAC=60°,∴∠C=30°,∴AC=2AB (1分)
设AB=k,则AC=2k,BC=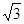 k,∵D为BC中点,∴BD=DC=
k,∵D为BC中点,∴BD=DC=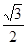 k
k
在Rt△ABD中,AB2+BD2=AD2,AD=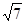
∴k2+(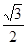 k)2=(
k)2=(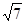 )2 (1分)
)2 (1分)
∴k=2 (1分)
∴AB=2,BC=2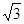 (1分)
(1分)
∴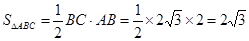 (1分)
(1分)
(2)∵AD⊥DE,∴∠ADE=90º,∴∠DAE+∠E=90º
∵∠ABC=90°,∴∠DAE+∠ADB=90°,∴∠ADB=∠E (1分)
∵∠ABD=∠DBE=90°,∴△ABD∽△DBE (1分)
∴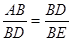 (1分)
(1分)
∴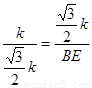 ,∴
,∴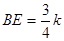 (1分)
(1分)
∴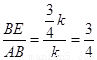 (1分)
(1分)
考点:直角三角形特殊角,边之间的关系,勾股定理,及三角形面积公式,相似三角形的判定及性质,
点评:(1)问,应用了直角三角形特殊角与边与边之间的关系,由题意求出边长易得到三角形的面积。(2)中根据已知可证得两个三角形相似,利用相似比,可求出,本题难度不大,属于基础题。

 教材全解字词句篇系列答案
教材全解字词句篇系列答案(本题满分10分)宏远商贸公司有A、B两种型号的商品需运出,这两种商品的体积和质量分别如下表所示:
|
(1)已知一批商品有A、B两种型号,体积一共是20 m3 ,质量一共是10.5吨,求A、B两种型号商品各有几件?
(2)物流公司现有可供使用的货车每辆额定载重3.5吨,容积为6 m3,其收费方式有以下两种:
①按车收费:每辆车运输货物到目的地收费600元;
②按吨收费:每吨货物运输到目的地收费200元.
要将(1)中的商品一次或分批运输到目的地,宏远商贸公司应如何选择运送、付费方式运费最少?并求出该方式下的运费是多少元?
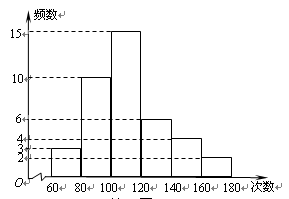
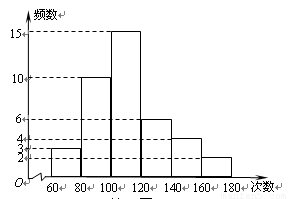
 秒跳绳的成绩,列出的频数分布直方图如下(每个分组包括左端点,不包括右端点),那么
秒跳绳的成绩,列出的频数分布直方图如下(每个分组包括左端点,不包括右端点),那么