题目内容
△ABC的三边均满足方程x2-6x+8=0,则它的周长为
- A.8或10
- B.10
- C.10或12或6
- D.6或8或10或12
C
分析:首先解一元二次方程x2-6x+8=0得:x1=2,x2=4,再根据三角形的三边关系确定三角形的三边长,分三种情况:①4,4,2;②2,2,2;③4,4,4;再根据三边长算周长即可.
解答:解方程x2-6x+8=0得:x1=2,x2=4,
∵△ABC的三边均满足方程x2-6x+8=0,
∴△ABC的三边长为:①4,4,2;②2,2,2;③4,4,4;
∴它的周长为:①4+4+2=10,②2+2+2=6,③4+4+4=12,
故选;C.
点评:此题主要考查了解一元二次方程以及三角形的三边关系,关键是掌握三角形的三边关系定理;三角形两边之和大于第三边.
分析:首先解一元二次方程x2-6x+8=0得:x1=2,x2=4,再根据三角形的三边关系确定三角形的三边长,分三种情况:①4,4,2;②2,2,2;③4,4,4;再根据三边长算周长即可.
解答:解方程x2-6x+8=0得:x1=2,x2=4,
∵△ABC的三边均满足方程x2-6x+8=0,
∴△ABC的三边长为:①4,4,2;②2,2,2;③4,4,4;
∴它的周长为:①4+4+2=10,②2+2+2=6,③4+4+4=12,
故选;C.
点评:此题主要考查了解一元二次方程以及三角形的三边关系,关键是掌握三角形的三边关系定理;三角形两边之和大于第三边.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
△ABC的三边均满足方程 ,则它的周长为( )
,则它的周长为( )
 ,则它的周长为( )
,则它的周长为( )| A.8或10 | B.10 | C.10或12或6 | D.6或8或10或12 |
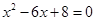 ,则它的周长为( )
,则它的周长为( )