Question

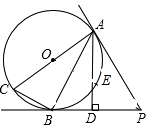
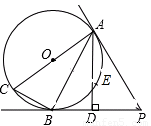
如图，AC是圆O的直径，PA切圆O于点A，弦BC∥OP，OP交圆O于点D，连接PB
（1）求证：PB是圆O的切线；
（2）若PA=3，PD=2，求圆O的半径R的长．

Answer 1

分析：（1）若要证明PB是圆O的切线，连接OB．证OB⊥PB即可．本题通过证明△POB≌△POA得证；
（2）因为PA是圆的切线，所以OA⊥AP，所以三角形AOP是直角三角形，由勾股定理可知，（R+2）²=R²+3²，解方程求出R的值即可．

解答：（1）证明：连接OB，
∵OP∥BC
∴∠AOP=∠C，∠BOP=∠OBC，
∵OB=OC，
∴∠C=∠OBC，
∴∠AOP=∠BOP，
∵OA=OB，OP=OP，
∴△AOP≌△BOP，
∴∠OBP=∠OAP，
∵PA切圆O于点A，
∴∠A=90°，
∴∠OBP=90°，
即OB⊥PB，
∴PB是圆O的切线，

（2）∵PA是圆的切线，
∴OA⊥AP，
∴△AOP是直角三角形，
在Rt△AOP中，由勾股定理得，（R+2）²=R²+3²
解得R=

5

4

．

点评：此题考查了切线的性质和判定、全等三角形的判定和性质、勾股定理，综合很性强，难度不大．