题目内容
方程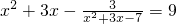 的全体实数根的积为
的全体实数根的积为
- A.60
- B.一60
- C.10
- D.一10
A
分析:设x2+3x-7=y,原方程化成y-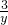 =2,再整理成整式方程求解即可.
=2,再整理成整式方程求解即可.
解答:设x2+3x-7=y,则y-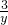 =2,
=2,
∴y2-2y-3=0,解得y1=-1,y2=3,
当y1=-1时,x2+3x-7=-1,解得x= ;
;
当y2=3时,x2+3x-7=3,解得x=2或-5;
∴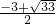 •
•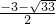 ×2×(-5)=60,
×2×(-5)=60,
故选A.
点评:本题考查了用换元法解分式方程,解次题的关键是把x2+3x-7看成一个整体来计算,即换元法思想.
分析:设x2+3x-7=y,原方程化成y-
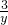 =2,再整理成整式方程求解即可.
=2,再整理成整式方程求解即可.解答:设x2+3x-7=y,则y-
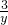 =2,
=2,∴y2-2y-3=0,解得y1=-1,y2=3,
当y1=-1时,x2+3x-7=-1,解得x=
 ;
;当y2=3时,x2+3x-7=3,解得x=2或-5;
∴
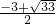 •
•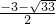 ×2×(-5)=60,
×2×(-5)=60,故选A.
点评:本题考查了用换元法解分式方程,解次题的关键是把x2+3x-7看成一个整体来计算,即换元法思想.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
方程x2+3x-
=9的全体实数根的积为( )
| 3 |
| x2+3x-7 |
| A、60 | B、一60 |
| C、10 | D、一10 |
 的全体实数根之积为 .
的全体实数根之积为 .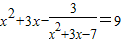 的全体实数根的积为( )
的全体实数根的积为( )