题目内容
若⊙O的直径AB为2,弦AC为| 2 |
| 3 |
分析:根据⊙O直径AB为2可知半径为1,根据弦AC为
,弦AD为
,连接BC、BD,易得:∠COD=150°或30°,所以根据扇形的面积公式得
=
,或
=
.
| 2 |
| 3 |
| 150π×1 |
| 360 |
| 5π |
| 12 |
| 30×π×1 |
| 360 |
| π |
| 12 |
解答: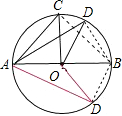 解:连接BC、BD,
解:连接BC、BD,
Rt△ABC中,AC=
,AB=2,因此∠CAB=45°,∠COB=90°.
同理可求得∠DAB=30°,∠BOD=60°.
①当AD、AC在AB一侧时,∠COD=∠COB-∠BOD=30°,
S扇形OCD=
=
;
②当AD、AC分别在AB两侧时,同①可求得∠COD=60+60+30=150°,
S扇形OCD=
=
.
 解:连接BC、BD,
解:连接BC、BD,Rt△ABC中,AC=
| 2 |
同理可求得∠DAB=30°,∠BOD=60°.
①当AD、AC在AB一侧时,∠COD=∠COB-∠BOD=30°,
S扇形OCD=
| 30π×1 |
| 360 |
| π |
| 12 |
②当AD、AC分别在AB两侧时,同①可求得∠COD=60+60+30=150°,
S扇形OCD=
| 150π×1 |
| 360 |
| 5π |
| 12 |
点评:本题的关键是利用直角三角形求出圆心角的度数,然后根据扇形面积计算公式进行求解.

练习册系列答案
相关题目
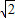 ,弦AD为
,弦AD为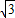 ,则S扇形OCD(其中,2S扇形OCD<S⊙O)为 .
,则S扇形OCD(其中,2S扇形OCD<S⊙O)为 .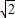 ,弦AD为
,弦AD为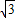 ,则S扇形OCD(其中,2S扇形OCD<S⊙O)为 .
,则S扇形OCD(其中,2S扇形OCD<S⊙O)为 .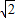 ,弦AD为
,弦AD为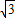 ,则S扇形OCD(其中,2S扇形OCD<S⊙O)为 .
,则S扇形OCD(其中,2S扇形OCD<S⊙O)为 .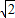 ,弦AD为
,弦AD为 ,则S扇形OCD(其中,2S扇形OCD<S⊙O)为 .
,则S扇形OCD(其中,2S扇形OCD<S⊙O)为 .