题目内容
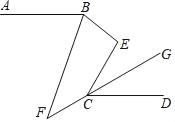
【题目】如图，AB是⊙O的直径，弦DC交AB于E，过C作⊙O的切线交DB的延长线于M，若AB=4，∠ADC=45°，∠M=75°，则CD的长为（ ）
A. 
B. 2 C. 
D. 
【答案】D
【解析】
连接OC，过O作OF⊥CD，构造垂径定理，利用已知的45°角，可以得到∠OCF度数，再利用垂径定理所构造的直角三角形，可得到CD长.
解：连接OC，过O作OF⊥CD，利用垂径定理得到F为CD的中点，
∵CM为圆O的切线，
∴∠OCM=90°，
∵∠ADC与∠AOC都对弧AC，
∴∠AOC=2∠ADC=90°，
∴∠CDM=
∠BOC=45°，
∵∠M=75°，
∴∠DCM=60°，
∴∠OCF=30°，
在Rt△OCF中，OC=2，
∴CF=OCcos∠OCF=
，
则CD=2CF=2．
故选：D．
练习册系列答案
相关题目
