题目内容
用水平线和竖起线将平面分成若干个边长为1的小正方形格子,小正方形的顶点称为格点,以格点为顶点的多边形称为格点多边形.设格点多边形的面积为S,该多边形各边上的格点个数和为a,内部的格点个数为b,则S=![]() a+b﹣1(史称“皮克公式”).
a+b﹣1(史称“皮克公式”).
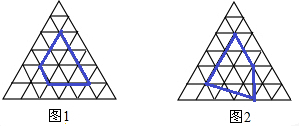
小明认真研究了“皮克公式”,并受此启发对正三角开形网格中的类似问题进行探究:正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,下图是该正三角形格点中的两个多边形:
根据图中提供的信息填表:
| 格点多边形各边上的格点的个数 | 格点边多边形内部的格点个数 | 格点多边形的面积 | |
| 多边形1 | 8 | 1 | |
| 多边形2 | 7 | 3 | |
| … | … | … | … |
| 一般格点多边形 | a | b | S |
则S与a、b之间的关系为S= a+2(b﹣1) (用含a、b的代数式表示).
考点:
规律型:图形的变化类.
分析:
根据8=8+2(1﹣1),11=7+2(3﹣1)得到S=a+2(b﹣1).
解答:
解:填表如下:
| 格点多边形各边上的格点的个数 | 格点边多边形内部的格点个数 | 格点多边形的面积 | |
| 多边形1 | 8 | 1 | 8 |
| 多边形2 | 7 | 3 | 11 |
| … | … | … | … |
| 一般格点多边形 | a | b | S |
则S与a、b之间的关系为S=a+2(b﹣1)(用含a、b的代数式表示).
点评:
考查了作图﹣应用与设计作图.此题需要根据图中表格和自己所算得的数据,总结出规律.寻找规律是一件比较困难的活动,需要仔细观察和大量的验算.

 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案用水平线和竖起线将平面分成若干个边长为1的小正方形格子,小正方形的顶点称为格点,以格点为顶点的多边形称为格点多边形.设格点多边形的面积为S,该多边形各边上的格点个数和为a,内部的格点个数为b,则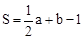 (史称“皮克公式”).
(史称“皮克公式”).
小明认真研究了“皮克公式”,并受此启发对正三角开形网格中的类似问题进行探究:正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,下图是该正三角形格点
中的两个多边形:
根据图中提供的信息填表:
|
|
格点多边形各边上的格点的个数 |
格点边多边形内部的格点个数 |
格点多边形的面积 |
|
多边形1 |
8 |
1 |
|
|
多边形2 |
7 |
3 |
|
|
… |
… |
… |
… |
|
一般格点多边形 |
a |
b |
S |
则S与a、b之间的关系为S= (用含a、b的代数式表示).
用水平线和竖起线将平面分成若干个边长为1的小正方形格子,小正方形的顶点称为格点,以格点为顶点的多边形称为格点多边形.设格点多边形的面积为S,该多边形各边上的格点个数和为a,内部的格点个数为b,则S= a+b-1(史称“皮克公式”).
a+b-1(史称“皮克公式”).
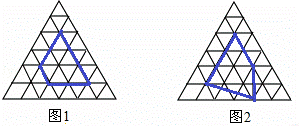
小明认真研究了“皮克公式”,并受此启发对正三角开形网格中的类似问题进行探究:正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,下图是该正三角形格点中的两个多边形:

根据图中提供的信息填表:
| 格点多边形各边上的格点的个数 | 格点边多边形内部的格点个数 | 格点多边形的面积 | |
| 多边形1 | 8 | 1 | |
| 多边形2 | 7 | 3 | |
| … | … | … | … |
| 一般格点多边形 | a | b | S |
 a+b-1(史称“皮克公式”).
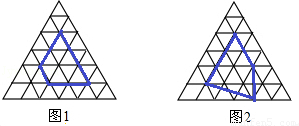
a+b-1(史称“皮克公式”).小明认真研究了“皮克公式”,并受此启发对正三角开形网格中的类似问题进行探究:正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,下图是该正三角形格点中的两个多边形:
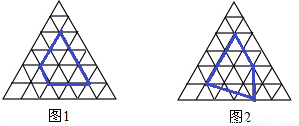
根据图中提供的信息填表:
| 格点多边形各边上的格点的个数 | 格点边多边形内部的格点个数 | 格点多边形的面积 | |
| 多边形1 | 8 | 1 | |
| 多边形2 | 7 | 3 | |
| … | … | … | … |
| 一般格点多边形 | a | b | S |