题目内容
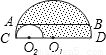
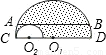
如图,大半圆O1与小半圆O2相切于点C,大半圆的弦AB与小半圆相切于点F,且AB∥CD,AB=4cm,则阴影部分的面积为 cm2.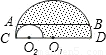
【答案】分析:阴影部分的面积等于大半圆面积减去小半圆面积,根据垂径定理和勾股定理求解.
解答: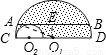 解:设大圆圆心为O1,作EO1⊥AB,垂足为E.
解:设大圆圆心为O1,作EO1⊥AB,垂足为E.
连接O1A,则O1A是大圆半径,
∵AB∥CD,
∴EO1的长等于小圆的半径,
由垂径定理知,点E是AB的中点.
由勾股定理知,O1A2-EO12=AE2=4,
∴阴影部分的面积= (O1A2-EO12)π=2π(cm2).
(O1A2-EO12)π=2π(cm2).
点评:本题利用了垂径定理和勾股定理,圆的面积公式求解.
解答:
 解:设大圆圆心为O1,作EO1⊥AB,垂足为E.
解:设大圆圆心为O1,作EO1⊥AB,垂足为E.连接O1A,则O1A是大圆半径,
∵AB∥CD,
∴EO1的长等于小圆的半径,
由垂径定理知,点E是AB的中点.
由勾股定理知,O1A2-EO12=AE2=4,
∴阴影部分的面积=
 (O1A2-EO12)π=2π(cm2).
(O1A2-EO12)π=2π(cm2).点评:本题利用了垂径定理和勾股定理,圆的面积公式求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
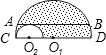 如图,大半圆O1与小半圆O2相切于点C,大半圆的弦AB与小半圆相切于点F,且AB∥CD,AB=4cm,则阴影部分的面积为
如图,大半圆O1与小半圆O2相切于点C,大半圆的弦AB与小半圆相切于点F,且AB∥CD,AB=4cm,则阴影部分的面积为 如图,大半圆O1与小半圆O2相切于点C,大半圆的弦AB与小半圆相切于点F,且AB∥CD,AB=4cm,则阴影部分的面积为________cm2.
如图,大半圆O1与小半圆O2相切于点C,大半圆的弦AB与小半圆相切于点F,且AB∥CD,AB=4cm,则阴影部分的面积为________cm2.