题目内容
【题目】对于有理数a、b,定义运算:“★”,当a≥b时,a★b=2a-3b,当a<b时,a★b=![]() .
.
(1)计算:(x+2)★(x+1)的值;
(2)若(x+1)★(2x-1)=-1,求x的值.
【答案】(1)-x+1(2)1.5
【解析】
(1)由于x+2>x+1,代入a★b=2a-3b计算即可求解;
(2)分x+1≥2x-1与x+1<2x-1两种情况,利用题中的新定义化简已知等式,求出方程的解即可得到x的值.
(1)(x+2)★(x+1)
=2(x+2)-3(x+1)
=2x+4-3x-3
=-x+1;
(2)当x+1≥2x-1时,
2(x+1)-3(2x-1)=-1,
2x+2-6x+3=-1,
2x-6x=-1-2-3,
-4x=-6,
x=1.5,
此时x+1=1.5+1=2.5,2x-1=3-1=2,
2.5>2,符合题意;
当x+1<2x-1时,
![]() +
+![]() =-1,
=-1,
3(x+1)+2(2x-1)=-6,
3x+3+4x-2=-6,
3x+4x=-6-3+2,
7x=-7,
x=-1,
此时x+1=-1+1=0,2x-1=-2-1=-3,
0>3,不符合题意.
故x的值为1.5.

【题目】“世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受人们的喜欢,各种品牌的山地自行车相继投放市场.顺风车行经营的A型车2015年6月份销售总额为3.2万元,2016年经过改造升级后A型车每辆销售价比2015年增加400元,若2016年6月份与2015年6月份卖出的A型车数量相同,则2016年6月份A型车销售总额将比2015年6月份销售总额增加25%.
(1)求2016年6月份A型车每辆销售价为多少元(用列方程的方法解答);
(2)该车行计划2016年7月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,A,B两种型号车的进货和销售价格如下表:
A型车 | B型车 | |
进货价格/(元/辆) | 1100 | 1400 |
销售价格/(元/辆) | 2016年的销售价格 | 2400 |
应如何进货才能使这批车获利最多?
【题目】某校举行了“文明在我身边”摄影比赛.已知每幅参赛作品成绩记为x分(60≤x<100).校方从600幅参赛作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制了如下不完整的统计图表.
分数段 | 频数 | 频率 |
60≤x<70 | 18 | 0.36 |
70≤x<80 | 17 | c |
80≤x<90 | a | 0.24 |
90≤x<100 | b | 0.06 |
合计 | 1 |
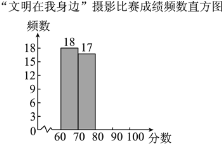
根据以上信息解答下列问题:
(1)统计表中c的值为________;样本成绩的中位数落在分数段________中;
(2)补全频数直方图;
(3)若80分以上(含80分)的作品将被组织展评,试估计全校被展评的作品数量是多少.