题目内容
如图，设P是凸四边形ABCD内的一点，过P分别作AB、BC、CD、DA的垂线，垂足分别为E、F、G、H．已知AH=3，HD=4，DG=1，GC=5，CF=6，FB=4，且BE-AE=1．则四边形ABCD的周长为34
34
．分析：此题根据勾股定理分别求出AP2、BP2、CP2、DP2，再把四式后一等号两边分别相加，并代入已知数值，最后进行化简，即可得出答案．
解答：解：由勾股定理可得：
AP2=AH2+PH2=AE2+PE2
BP2=BE2+PE2=BF2+PF2
CP2=CF2+PF2=CG2+PG2
DP2=DG2+PG2=DH2+PH2
以上四式后一等号两边分别相加，并代入已知数值可得：
9+BE2+36+1=AE2+16+25+16
化简得：BE2-AE2=11，即（BE+AE）（BE-AE）=11，
又已知：BE-AE=1，
解得：BE=6，AE=5，
故周长为34．
故填：34．
AP2=AH2+PH2=AE2+PE2
BP2=BE2+PE2=BF2+PF2
CP2=CF2+PF2=CG2+PG2
DP2=DG2+PG2=DH2+PH2
以上四式后一等号两边分别相加，并代入已知数值可得：
9+BE2+36+1=AE2+16+25+16
化简得：BE2-AE2=11，即（BE+AE）（BE-AE）=11，
又已知：BE-AE=1，
解得：BE=6，AE=5，
故周长为34．
故填：34．
点评：此题考查了勾股定理；解题的关键根据勾股定理列出等式，再进行化简整理．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
品学双优卷系列答案
小学期末冲刺100分系列答案
相关题目
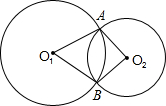如图，⊙O1与⊙O2相交于点A、B，顺次连接O1、A、O2、B四点，得四边形O1AO2B．
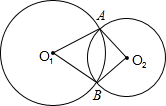如图，⊙O1与⊙O2相交于点A、B，顺次连接O1、A、O2、B四点，得四边形O1AO2B．
如图，设P是凸四边形ABCD内的一点，过P分别作AB、BC、CD、DA的垂线，垂足分别为E、F、G、H．已知AH=3，HD=4，DG=1，GC=5，CF=6，FB=4，且BE-AE=1．则四边形ABCD的周长为________．