题目内容
(2003•海淀区)已知二次函数y=kx2+(2k-1)x-1与x轴交点的横坐标为x1、x2(x1<x2),则对于下列结论:①当x=-2时,y=1;②当x>x1时,y>0;③方程kx2+(2k-1)x-1=0有两个不相等的实数根x1、x2;④x1<-1,x2>-1;⑤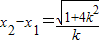 ,其中所有正确的结论是 (只需填写序号).
,其中所有正确的结论是 (只需填写序号).
【答案】分析:把相应的x的值代入;二次函数与x轴的交点即为转换为一元二次方程等于0的解;与-1相关就加上1后应用相关不等式整理结果;两根相减需确定二次项系数的符号.
解答:解:<1>把x=-2直接代入函数式可得y=1,正确;
<2>因不知道k的符号,就不知道开口方向,无法确定,错误;
<3>因二次函数y=kx2+(2k-1)x-1与x轴有两个交点,所以,方程kx2+(2k-1)x-1=0有两个不相等的实数根x1、x2,正确;
<4>∵(x1+1)(x2+1)=x1x2+x1+x2+1=- -
-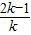 +1=-1<0,又x1<x2,
+1=-1<0,又x1<x2,
∴x1+1<x2+1,x1+1<0,x2+1>0,即x1<-1,x2>-1,正确;
<5>因为k的符号不确定,无法知道x2-x1的大小,错误.
∴正确的结论是<1>、<3>、<4>.
点评:主要考查了二次函数的性质与一元二次方程的根,及根与系数之间的关系.
解答:解:<1>把x=-2直接代入函数式可得y=1,正确;
<2>因不知道k的符号,就不知道开口方向,无法确定,错误;
<3>因二次函数y=kx2+(2k-1)x-1与x轴有两个交点,所以,方程kx2+(2k-1)x-1=0有两个不相等的实数根x1、x2,正确;
<4>∵(x1+1)(x2+1)=x1x2+x1+x2+1=-
 -
-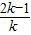 +1=-1<0,又x1<x2,
+1=-1<0,又x1<x2,∴x1+1<x2+1,x1+1<0,x2+1>0,即x1<-1,x2>-1,正确;
<5>因为k的符号不确定,无法知道x2-x1的大小,错误.
∴正确的结论是<1>、<3>、<4>.
点评:主要考查了二次函数的性质与一元二次方程的根,及根与系数之间的关系.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
(2003•海淀区)某同学在测量体温时意识到体温计的读数与水银柱的长度之间可能存在着某种函数关系,就此他与同学们选择了一种类型的体温计,经历了收集数据、分析数据、得出结论的探索过程,他们收集到的数据如下:
请你根据上述数据分析判断,水银柱的长度l(mm)与体温计的读数t(℃)(35≤t≤42)之间存在的函数关系是( )
A.
B.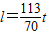
C.
D.
| 体温计的读数t(℃) | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 |
| 水银柱的长度l(mm) | 56.5 | 62.5 | 68.5 | 74.5 | 80.5 | 86.5 | 92.5 | 98.5 |
A.

B.
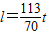
C.

D.


 的图象经过点(1,2),则函数y=-kx可为( )
的图象经过点(1,2),则函数y=-kx可为( )

 的图象经过点(1,2),则函数y=-kx可为( )
的图象经过点(1,2),则函数y=-kx可为( )

 ,其中a、b、c分别为△ABC中∠A,∠B,∠C的对边.
,其中a、b、c分别为△ABC中∠A,∠B,∠C的对边. ,若△ABC的周长为10,求抛物线的解析式;
,若△ABC的周长为10,求抛物线的解析式; 交于点E、F,与y轴交于点M,且抛物线对称轴为x=a,O是坐标原点,△MOE与△MOF的面积之比为5:1,试判断△ABC的形状并证明你的结论.
交于点E、F,与y轴交于点M,且抛物线对称轴为x=a,O是坐标原点,△MOE与△MOF的面积之比为5:1,试判断△ABC的形状并证明你的结论.