Question

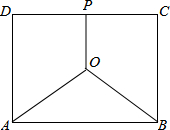某地有三家工厂，分别位于矩形ABCD的顶点A、B及边CD的中点P处，已知AB=16km，BC=12km，为了处理三家工厂的污水，现要在矩形ABCD的区域上（含边界），且与A，B等距离的一点O处建造一个污水处理厂，并铺设排污管道AO，BO，OP．记管道总长为S km．下列说法正确的是（　　）

• A、S的最小值是8

  13

• B、S的最小值应该大于28
• C、S的最小值是26
• D、S的最小值应该小于26

Answer 1

分析：根据题意表示出PO的长，再利用特殊值法确定S的最小值的范围即可．

解答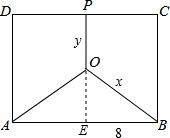：解：过点O作OE⊥AB于点E，
∵AO=BO，
∴AE=BE=8，
∴EO=

x2-82

，
∴y=12-

x2-82

，
∴S=y+2x=12-

x2-82

+2x，
当x=9时，S=12-

17

+18≈25.88，
∴S的最小值应该小于26．
故选：D．

点评：此题主要考查了应用设计与作图，得出S与x的函数关系式是解题关键．