题目内容
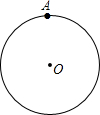如图，一个直径是4的⊙O中． （1）请以A为圆心画出一个圆心角为90°的扇形BAC交⊙O于B、C 两点；
（2）求这个扇形BAC的面积（结果保留π）．
分析：（1）连接OA，作直径BC⊥OA，则以A为圆心，以AB为半径作
，连接AB、AC即可所求的扇形；
（2）利用扇形的面积公式即可求解．
 |
| BC |
（2）利用扇形的面积公式即可求解．
解答：
解：（1）扇形BAC即为所求的扇形；
（2）在直角△OAB中，AB=
=2
．
扇形的面积是：
=2π．
解：（1）扇形BAC即为所求的扇形；（2）在直角△OAB中，AB=
| 22+22 |
| 2 |
扇形的面积是：
90π•(2
| ||
| 360 |
点评：本题考查了圆周角定理，正确利用直径所对的圆周角是直角，确定B，C的位置是解题的关键．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
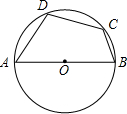已知：如图，四边形ABCD是⊙O的内接四边形，AB是⊙O的直径．若再增加一个条件，就可使四边形ABCD成为等腰梯形．你所增加的条件是：
如图，一个直径是4的⊙O中． 
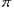表示)。