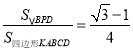题目内容
【题目】某城市绿化工程进行招标，现有甲、乙两个工程队投标，已知甲队单独完成这项工程需要60天.经测算：如果甲队先做20天，再由甲队、乙队合作12天，那么此时共完成总工作量的
．
（1）乙队单独完成这项工程需要多少天？
（2）甲队施工一天需付工程款4.5万元，乙队施工一天需付工程款2万元，该工程由甲乙两队合作若干天后，再由乙队完成剩余的工作，若要求完成此项工程的工程款不超过186万元，求甲、乙两队最多合作多少天？
【答案】（1）90天（2）4天
【解析】
（1）设乙队单独完成这项工程需要x天，根据甲队完成的工作量＋乙队完成的工作量＝总工作量的三分之二，即可得出关于x的分式方程，解之经检验后即可得出结论；
（2）设甲、乙两队合作m天，则乙队还需单独工作[（1
）÷
]天才可完工，根据总工程款＝4.5×甲队工作时间＋2×乙队工作时间结合工程款不超过186万元，即可得出关于m的一元一次不等式，解之取其最大值即可得出结论．
（1）设乙队单独完成这项工程需要x天，
依题意，得：
，
解得：x＝90，
经检验，x＝90是原方程的解，且符合题意．
答：乙队单独完成这项工程需要90天．
（2）设甲、乙两队合作m天，则乙队还需单独工作 [（1）÷]天才可完工，
依题意，得：4.5m＋2[m＋（1）÷]≤186，
整理，得：1.5m＋180≤186，
解得：m≤4．
答：甲、乙两队最多合作4天．
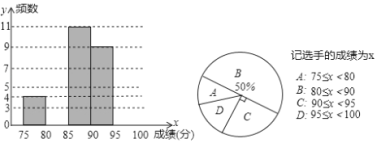
阅读快车系列答案
【题目】为了庆祝中华人民共和国成立70周年，某市决定开展“我和祖国共成长”主题演讲比赛，某中学将参加本校选拔赛的40名选手的成绩(满分为100分，得分为正整数且无满分，最低为75分)分成五组，并绘制了下列不完整的统计图表．
分数段 | 频数 | 频率 |
74.5～79.5 | 2 | 0.05 |
79.5～84.5 | m | 0.2 |
84.5～89.5 | 12 | 0.3 |
89.5～94.5 | 14 | n |
94.5～99.5 | 4 | 0.1 |
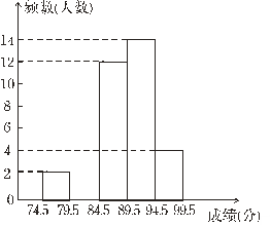
(1)表中m＝ ，n＝ ；
(2)请在图中补全频数直方图；
(3)甲同学的比赛成绩是40位参赛选手成绩的中位数，据此推测他的成绩落在 分数段内；
(4)选拔赛中，成绩在94.5分以上的选手，男生和女生各2人，学校从中随机确定2名选手参加全市决赛，恰好是一名男生和一名女生的概率是 ．
