题目内容
如图，以△ABC的各边为边分别向外作正方形，所得到的三个正方形的面积分别为S1=36，S2=64，S3=100，则△ABC的面积是
- A.12
- B.48
- C.24
- D.3
C
分析：由正方形的面积公式可知：S1=36=AC2，S2=64=BC2，S3=100=AB2，利用勾股定理的逆定理可知△ABC为直角三角形，同时可求出AC、AB和BC的长，最后根据三角形的面积公式求解即可．
解答：∵由正方形面积公式得：S1=36=AC2，S2=64=BC2，S3=100=AB2，
∴AC2+BC2=AB2，AC=6，BC=8，AB=10，
故△ABC为直角三角形．
∴S△ABC=
×AC×BC=×6×8=24．
故选C．
点评：本题考查了勾股定理的逆定理及正方形面积公式的运用，解题关键是明确此题中直角三角形的边长的平方即为相应的正方形的面积，难度一般．
分析：由正方形的面积公式可知：S1=36=AC2，S2=64=BC2，S3=100=AB2，利用勾股定理的逆定理可知△ABC为直角三角形，同时可求出AC、AB和BC的长，最后根据三角形的面积公式求解即可．
解答：∵由正方形面积公式得：S1=36=AC2，S2=64=BC2，S3=100=AB2，
∴AC2+BC2=AB2，AC=6，BC=8，AB=10，
故△ABC为直角三角形．
∴S△ABC=
×AC×BC=×6×8=24．故选C．
点评：本题考查了勾股定理的逆定理及正方形面积公式的运用，解题关键是明确此题中直角三角形的边长的平方即为相应的正方形的面积，难度一般．
练习册系列答案
相关题目
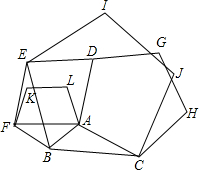（2012•拱墅区一模）如图，以△ABC的各边为边，在BC的同侧分别作三个正五边形．它们分别是正五边形ABFKL、BCJIE、ACHGD，试探究：
如图，以△ABC的各边为边分别向外作正方形，所得到的三个正方形的面积分别为S1=36，S2=64，S3=100，则△ABC的面积是（ ）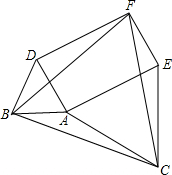
如图，以△ABC的各边为一边向BC的同侧作正△ABD、正△BCF、正△ACE，若∠BAC=150°，求证：四边形AEFD为矩形．
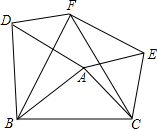如图，以△ABC的各边向同侧作正三角形，即等边△ABD、△BCF、△ACE．
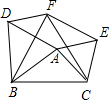如图，以△ABC的各边向同侧作正△ABD，BCF，ACE．