题目内容
【题目】如图,以BC为直径的圆交△ABC的两边AB、AC于点D、E,点E恰为AC的中点,BF为△ABC的外角平分线,点F在圆上,请你仅用一把无刻度的直尺,过点A作一条线段,将△ABC分成面积相等的两部分. 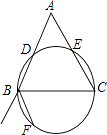
【答案】解:如图,连接BE,EF交直径BC于点O,即点O为圆的圆心,连接AO,即为所求作的线段. 
理由:∵BC为圆的直径,
∴BE⊥AC,
∵点E是AC中点,
∴∠ABE=∠CBE= ![]() ∠ABC,
∠ABC,
∵BF为△ABC的外角的平分线,
∴∠CBF= ![]() ∠CBG,
∠CBG,
∴∠EBF=∠EBC+∠CBF= ![]() (∠ABC+∠CBG)=90°,
(∠ABC+∠CBG)=90°,
∵BC为直径,
∴∠BFC=90°,
∴∠BEC=∠EBF=∠BFC=90°,
∴四边形EBFC是矩形,
∴点O是BC中点,即:为圆心;
∴AO是△ABC的边BC中线,
即:AO将△ABC分成面积相等的两部分,
【解析】利用等腰三角形的三线合一,判断出BE是∠ABC的平分线,进而判断出∠EBF=90°,再判断出四边形EBFC是矩形,点O为矩形对角线的交点即可.

练习册系列答案
相关题目
【题目】某校实施课程改革,为初三学生设置了A,B,C,D,E,F共六门不同的拓展性课程,现随机抽取若干学生进行了“我最想选的一门课”调查,并将调查结果绘制成如图统计图表(不完整)
选修课 | A | B | C | D | E | F |
人数 | 20 | 30 |
根据图标提供的信息,下列结论错误的是( )

A. 这次被调查的学生人数为200人 B. 扇形统计图中E部分扇形的圆心角为72°
C. 被调查的学生中最想选F的人数为35人 D. 被调查的学生中最想选D的有55人