题目内容
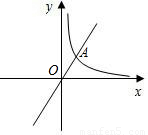
如图,正比例函数 与反比例函数
与反比例函数 的图象相交于A、B两点,过B作BC⊥x轴,垂足为C,且△BOC的面积等于4.
的图象相交于A、B两点,过B作BC⊥x轴,垂足为C,且△BOC的面积等于4.(1)求k的值;
(2)求A、B两点的坐标;
(3)在x轴的正半轴上是否存在一点P,使得△POA为直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】分析:(1)用B点坐标表示△BOC的面积建立关系式求k;
(2)解由函数解析式组成的方程组;
(3)存在.分别以OA为斜边和直角边分类讨论.
解答: 解:(1)设点B(x,y),则BC=|y|=-y,CO=|x|=-x,
解:(1)设点B(x,y),则BC=|y|=-y,CO=|x|=-x,
∵B(x,y)在反比例函数 的图象上,
的图象上,
∴xy=k,因△BOC的面积等于4, ,
,
∴k=8;
(2)∵k=8,所以反比例函数的解析式为 ,
,
解方程组: ,得:x1=4,y1=2;x2=-4,y2=-2,
,得:x1=4,y1=2;x2=-4,y2=-2,
∴点A(4,2),B(-4,-2);
(3)存在.
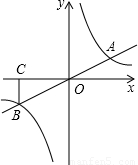
当AP⊥x轴时,如图(1)点P(4,0),
当AP⊥AO时,如图(2)设P(m,0),过点A作AD⊥x轴于D,
由A(4,2)得AD=2,DO=4,PD=m-4,
在Rt△ADO中,AO2=AD2+DO2=20,
在Rt△ADP中,AP2=AD2+DP2=4+(m-4)2,
在Rt△AOP中,PO2=AO2+AP2,
即:20+[4+(m-4)2]=m2,解得m=5,
所以P(5,0),
综上,在x轴上存在点P(4,0)或P(5,0),使得△POA为直角三角形.
点评:注意点的坐标与线段长度的联系;分类讨论思想的应用,培养严谨的思维习惯.
(2)解由函数解析式组成的方程组;
(3)存在.分别以OA为斜边和直角边分类讨论.
解答:
 解:(1)设点B(x,y),则BC=|y|=-y,CO=|x|=-x,
解:(1)设点B(x,y),则BC=|y|=-y,CO=|x|=-x,∵B(x,y)在反比例函数
 的图象上,
的图象上,∴xy=k,因△BOC的面积等于4,
 ,
,∴k=8;
(2)∵k=8,所以反比例函数的解析式为
 ,
,解方程组:
 ,得:x1=4,y1=2;x2=-4,y2=-2,
,得:x1=4,y1=2;x2=-4,y2=-2,∴点A(4,2),B(-4,-2);
(3)存在.
当AP⊥x轴时,如图(1)点P(4,0),
当AP⊥AO时,如图(2)设P(m,0),过点A作AD⊥x轴于D,
由A(4,2)得AD=2,DO=4,PD=m-4,
在Rt△ADO中,AO2=AD2+DO2=20,
在Rt△ADP中,AP2=AD2+DP2=4+(m-4)2,
在Rt△AOP中,PO2=AO2+AP2,
即:20+[4+(m-4)2]=m2,解得m=5,
所以P(5,0),
综上,在x轴上存在点P(4,0)或P(5,0),使得△POA为直角三角形.
点评:注意点的坐标与线段长度的联系;分类讨论思想的应用,培养严谨的思维习惯.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
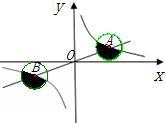 11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为
11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为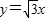 与反比例函数
与反比例函数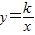 (k≠0)的图象在第一象限内交于点A,且AO=2,则k= .
(k≠0)的图象在第一象限内交于点A,且AO=2,则k= .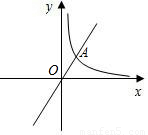
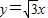 与反比例函数
与反比例函数 (k≠0)的图象在第一象限内交于点A,且AO=2,则k= .
(k≠0)的图象在第一象限内交于点A,且AO=2,则k= .