题目内容
如图3,在△ABC中,AB=AC,AD∥BC,如果∠BAC∶∠CAD=1∶2,那么∠B=_____度.

72
由AD∥BC,推出∠DAC=∠C,根据等腰三角形的性质得到∠B=∠C,即∠B=∠C=∠DAC,设∠BAC=x,根据三角形的内角和定理得到x+2x+2x=180°,求出x即可得到答案。
∵AD∥BC, ∴∠DAC=∠C,
∵AB=AC, ∴∠B=∠C, ∴∠B=∠C=∠DAC,
设∠BAC=x,则∠DAC=∠B=∠C=2x,
∵∠BAC+∠B+∠C=180°, ∴x+2x+2x=180°,
解得:x=36°, ∴∠B=72°,
故答案为:72°。
∵AD∥BC, ∴∠DAC=∠C,
∵AB=AC, ∴∠B=∠C, ∴∠B=∠C=∠DAC,
设∠BAC=x,则∠DAC=∠B=∠C=2x,
∵∠BAC+∠B+∠C=180°, ∴x+2x+2x=180°,
解得:x=36°, ∴∠B=72°,
故答案为:72°。

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
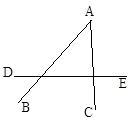

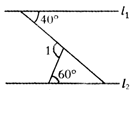

 被第三条直线所截,若同位角相等,则这两条直线
被第三条直线所截,若同位角相等,则这两条直线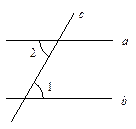

 ,
, ,则
,则 .
.