题目内容
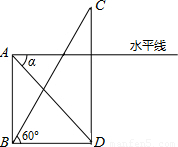
如图,小明在自己家的楼房AB的底部B测得大楼CD的顶部C的仰角∠CBD=60°,然后又在楼顶A处测得大楼的底部D的俯角α=55°,已知小明家的楼房高度AB=30米.求大楼的高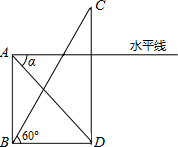 度CD(精确到0.1米).(以下数据供计算时选用:sin55°=0.8192,cos55°=0.5736,tan55°=1.428,cot55°=0.700,
度CD(精确到0.1米).(以下数据供计算时选用:sin55°=0.8192,cos55°=0.5736,tan55°=1.428,cot55°=0.700,| 2 |
| 3 |
分析:首先分析图形,根据题意构造直角三角形.本题涉及多个直角三角形,应利用其公共边构造三角关系,进而可求出答案.
解答:解:在Rt△ABD中,∠ABD=90°,∠BDA=α=55°,
∴BD=AB•cot∠BDA=30×cot55°.(3分)
在Rt△BDC中,∠BDC=90°,∠CBD=60°,
∴CD=BD•tan60°=30×cot55°•tan60°=30×0.700×
≈36.4米.
答:大楼的高度CD约为36.4米.
∴BD=AB•cot∠BDA=30×cot55°.(3分)
在Rt△BDC中,∠BDC=90°,∠CBD=60°,
∴CD=BD•tan60°=30×cot55°•tan60°=30×0.700×
| 3 |
答:大楼的高度CD约为36.4米.
点评:考查了解直角三角形的应用-仰角俯角问题,本题要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
 25、小明家想要在自己家的阳台上铺地砖,经测量后设计了如图的图纸,黑色区域为宽度相等的一条“7”形的健身用鹅卵石小路,空白部分为地砖铺设区域.要使铺地砖的面积为14平方米.
25、小明家想要在自己家的阳台上铺地砖,经测量后设计了如图的图纸,黑色区域为宽度相等的一条“7”形的健身用鹅卵石小路,空白部分为地砖铺设区域.要使铺地砖的面积为14平方米.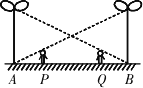
 度CD(精确到0.1米).(以下数据供计算时选用:sin55°=0.8192,cos55°=0.5736,tan55°=1.428,cot55°=0.700,
度CD(精确到0.1米).(以下数据供计算时选用:sin55°=0.8192,cos55°=0.5736,tan55°=1.428,cot55°=0.700, ,
,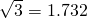 .)
.) ,
, .)
.)